题目内容
【题目】设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13． （Ⅰ）求{an}、{bn}的通项公式；
（Ⅱ）求数列 
的前n项和Sn ．
【答案】解：（Ⅰ）设{an}的公差为d，{bn}的公比为q，则依题意有q＞0且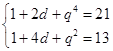 
解得d=2，q=2．
所以an=1+（n﹣1）d=2n﹣1，bn=qn﹣1=2n﹣1 ．
（Ⅱ） 
，
，①
Sn= 
，②
① ﹣②得 Sn=1+2（ + 
+…+ 
）﹣ 
，
则 
= 
= 
= 
．
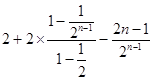【解析】（Ⅰ）设{an}的公差为d，{bn}的公比为q，根据等比数列和等差数列的通项公式，联立方程求得d和q，进而可得{an}、{bn}的通项公式．（Ⅱ）数列 
的通项公式由等差和等比数列构成，进而可用错位相减法求得前n项和Sn ．
【考点精析】本题主要考查了等差数列的通项公式（及其变式）和等比数列的通项公式（及其变式）的相关知识点，需要掌握通项公式：
或
；通项公式：
才能正确解答此题．
每课必练系列答案
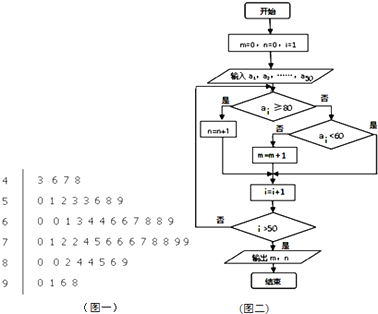
【题目】某学校为了解该校高三年级学生数学科学习情况，对广一模考试数学成绩进行分析，从中抽取了n 名学生的成绩作为样本进行统计（该校全体学生的成绩均在[60，140），按照[60，70），[70，80），[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）的分组作出频率分布直方图如图1所示，样本中分数在[70，90）内的所有数据的茎叶图如图2所示． 
根据上级统计划出预录分数线，有下列分数与可能被录取院校层次对照表为表（ c ）．
分数 | [50，85] | [85，110] | [110，150] |
可能被录取院校层次 | 专科 | 本科 | 重本 |
（1）求n和频率分布直方图中的x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为概率，若在该校高三年级学生中任取3 人，求至少有一人是可能录取为重本层次院校的概率；
（3）在选取的样本中，从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研，用ξ表示所抽取的3 名学生中为重本的人数，求随机变量ξ的分布列和数学期望．
