题目内容
设 ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且 ,则a2007=
,则a2007=
- A.

- B.

- C.

- D.

D
分析:先根据递推关系式得到fn+1(x)= ,再得到fn+1(x)+2、fn+1(x)-1的值后相比得到∴{
,再得到fn+1(x)+2、fn+1(x)-1的值后相比得到∴{ }是以
}是以 为首项以-2为公比的等比数列,故可得到{an}是以
为首项以-2为公比的等比数列,故可得到{an}是以 为首项以-
为首项以- 为公比的等比数列,进而可得到答案.
为公比的等比数列,进而可得到答案.
解答:∵fn+1(x)=f1[fn(x)]=
∴fn+1(x)+2= ,fn+1(x)-1=
,fn+1(x)-1=
∴
∴{ }是以
}是以 为首项以-2为公比的等比数列,
为首项以-2为公比的等比数列,
故{an}是以 =
= 为首项以-
为首项以- 为公比的等比数列
为公比的等比数列
∴∴a2007=
故选D.
点评:本题主要考查递推关系式的应用和等比数列的通项公式.考查综合运用能力.
分析:先根据递推关系式得到fn+1(x)=
 ,再得到fn+1(x)+2、fn+1(x)-1的值后相比得到∴{
,再得到fn+1(x)+2、fn+1(x)-1的值后相比得到∴{ }是以
}是以 为首项以-2为公比的等比数列,故可得到{an}是以
为首项以-2为公比的等比数列,故可得到{an}是以 为首项以-
为首项以- 为公比的等比数列,进而可得到答案.
为公比的等比数列,进而可得到答案.解答:∵fn+1(x)=f1[fn(x)]=

∴fn+1(x)+2=
 ,fn+1(x)-1=
,fn+1(x)-1=
∴

∴{
 }是以
}是以 为首项以-2为公比的等比数列,
为首项以-2为公比的等比数列,故{an}是以
 =
= 为首项以-
为首项以- 为公比的等比数列
为公比的等比数列∴∴a2007=

故选D.
点评:本题主要考查递推关系式的应用和等比数列的通项公式.考查综合运用能力.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且 ,则a2010=( )
,则a2010=( )



 ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且 ,则a2010=( )
,则a2010=( )



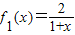 ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且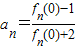 ,则a2010=
,则a2010=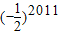 .
. ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且 ,则a2007=( )
,则a2007=( )


