题目内容
1．若${∫}_{1}^{e}$$\frac{1}{x}$dx=a，则（1-x）3（1-$\frac{a}{x}$）3展开式中的常数项是20．分析 求定积分得到a值，代入（1-x）3（1-$\frac{a}{x}$）3，展开两数差的立方公式后即可求得答案．
解答 解：由${∫}_{1}^{e}$$\frac{1}{x}$dx=$lnx{|}_{1}^{e}=1=a$，得a=1，
∴（1-x）3（1-$\frac{a}{x}$）3 =（1-x）3（1-$\frac{1}{x}$）3 =$（1-3x+3{x}^{2}-{x}^{3}）（1-\frac{3}{x}+\frac{3}{{x}^{2}}-\frac{1}{{x}^{3}}）$，
∴（1-x）3（1-$\frac{a}{x}$）3展开式中的常数项是1+9+9+1=20．
故答案为：20．
点评 本题考查二项式系数的性质，考查定积分的求法，训练了两数差的立方公式的应用，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，扇形AOB中，圆心角AOB的大小等于$\frac{π}{3}$，半径为2，在半径OA上有一动点C，过点C作平行于OB的直线交弧AB于点P．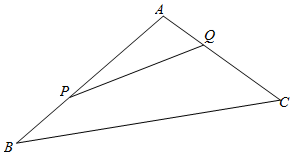
如图，上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区．已知∠A=120°，AB、AC的长度均大于200米．设AP=x，AQ=y，且AP，AQ总长度为200米．
13．下列命题的逆命题为真命题的是（ ）
| A． | 若x＞2，则（x-2）（x+1）＞0 | B． | 若x2+y2≥4，则xy=2 | ||
| C． | 若x+y=2，则xy≤l | D． | 若a≥b，则ac2≥bc2 |