题目内容
已知{an}为递减的等比数列,且{a1,a2,a3}?{-4,-3,-2,0,1,2,3,4}.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)当
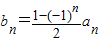 时,求证:b1+b2+b3+…+
时,求证:b1+b2+b3+…+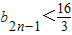 .
.
【答案】分析:(Ⅰ)由数列是递减的等比数列得q是正数,再从集合求出前三项,求出q代入通项公式即可;
(2)由(1)求出bn,并对n分类讨论:n=2k和n=2k-1化简bn,代入不等式的左边由等比数列的前n项和公式化简,再进行证明.
解答:解:(Ⅰ)∵{an}是递减数列,∴数列{an}的公比q是正数,
∵{a1,a2,a3}?{-4,-3,-2,0,1,2,3,4},
∴a1=4,a2=2,a3=1,∴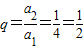 ,
,
∴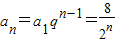 .
.
(Ⅱ)由(1)得, ,
,
当n=2k(k∈N*)时,bn=0,
当n=2k-1(k∈N*)时,bn=an,
即
∴b1+b2+b3+…+b2n-2+b2n-1=a1+a3+…+a2n-1
=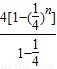
=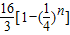
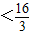 .
.
点评:本题考查了等比数列是递减数列的特点,通项公式和前n项和公式应用,考查了分类讨论思想.
(2)由(1)求出bn,并对n分类讨论:n=2k和n=2k-1化简bn,代入不等式的左边由等比数列的前n项和公式化简,再进行证明.
解答:解:(Ⅰ)∵{an}是递减数列,∴数列{an}的公比q是正数,
∵{a1,a2,a3}?{-4,-3,-2,0,1,2,3,4},
∴a1=4,a2=2,a3=1,∴
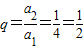 ,
,∴
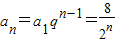 .
.(Ⅱ)由(1)得,
 ,
,当n=2k(k∈N*)时,bn=0,
当n=2k-1(k∈N*)时,bn=an,
即

∴b1+b2+b3+…+b2n-2+b2n-1=a1+a3+…+a2n-1
=
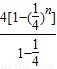
=
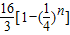
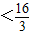 .
.点评:本题考查了等比数列是递减数列的特点,通项公式和前n项和公式应用,考查了分类讨论思想.

练习册系列答案
相关题目