题目内容
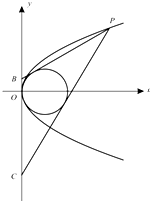 如图,P是抛物线y2=2x上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.
如图,P是抛物线y2=2x上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.分析:设P(x0,y0),B(0,b),C(0,c),设b>c.直线PB:y-b=
x,化简,得(y0-b)x-x0y+x0b=0,由圆心(1,0)到直线PB的距离是1,知
=1,由此导出(x0-2)b2+2y0b-x0=0,同理,(x0-2)c2+2y0c-x0=0,所以(b-c)2=
,从而得到S△PBC=
(b-c)x0,由此能求出△PBC面积的最小值.
| y0-b |
| x0 |
| |y0-b+x0b| | ||
|
| 4x02+4y02-8x0 |
| (x0-2)2 |
| 1 |
| 2 |
解答:解:设P(x0,y0),B(0,b),C(0,c),设b>c.
直线PB的方程:y-b=
x,
化简,得(y0-b)x-x0y+x0b=0,
∵圆心(1,0)到直线PB的距离是1,
∴
=1,
∴(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
∵x0>2,上式化简后,得
(x0-2)b2+2y0b-x0=0,
同理,(x0-2)c2+2y0c-x0=0,
∴b+c=
,bc=
,
∴(b-c)2=
,
∵P(x0,y0)是抛物线上的一点,
∴y02=2x0,
∴(b-c)2=
,b-c=
,
∴S△PBC=
(b-c)x0
=
•x0
=(x0-2)+
+4
≥2
+4=8.
当且仅当x0-2=
时,取等号.
此时x0=4,y0=±2
.
∴△PBC面积的最小值为8.
直线PB的方程:y-b=
| y0-b |
| x0 |
化简,得(y0-b)x-x0y+x0b=0,
∵圆心(1,0)到直线PB的距离是1,
∴
| |y0-b+x0b| | ||
|
∴(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
∵x0>2,上式化简后,得
(x0-2)b2+2y0b-x0=0,
同理,(x0-2)c2+2y0c-x0=0,
∴b+c=
| -2y0 |
| x0-2 |
| -x0 |
| x0-2 |
∴(b-c)2=
| 4x02+4y02-8x0 |
| (x0-2)2 |
∵P(x0,y0)是抛物线上的一点,
∴y02=2x0,
∴(b-c)2=
| 4x02 |
| (x0-2)2 |
| 2x0 |
| x0-2 |
∴S△PBC=
| 1 |
| 2 |
=
| x0 |
| x0-2 |
=(x0-2)+
| 4 |
| x0-2 |
≥2
| 4 |
当且仅当x0-2=
| 4 |
| x0-2 |
此时x0=4,y0=±2
| 2 |
∴△PBC面积的最小值为8.
点评:本昰考查三角形面积的最小值的求法,具体涉及到抛物线的性质、抛物线和直线的位置关系、圆的简单性质、均值定理等基本知识,综合性强,难度大,对数学思想的要求较高,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目