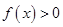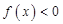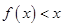题目内容
已知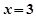 是函数
是函数 的一个极值点。
的一个极值点。
(1)求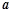 的值;
的值;
(2)求函数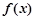 的单调区间;
的单调区间;
(3)若直线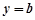 与函数
与函数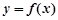 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。
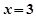 是函数
是函数 的一个极值点。
的一个极值点。(1)求
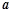 的值;
的值;(2)求函数
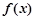 的单调区间;
的单调区间;(3)若直线
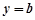 与函数
与函数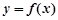 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。解:(1)因为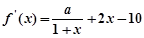 。。。。。。。1分
。。。。。。。1分
所以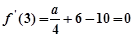 , 因此
, 因此 。。。。。。。2分
。。。。。。。2分
(2)由(1)知,
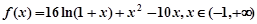
 。。。。。。。3分
。。。。。。。3分
当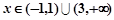 时,
时, 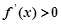
当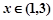 时,
时,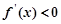 。。。。。。。4分
。。。。。。。4分
所以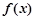 的单调增区间是
的单调增区间是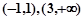
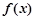 的单调减区间是
的单调减区间是 。。。。。。。5分
。。。。。。。5分
(3)由(2)知,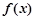 在
在 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在 上单调增加,且当
上单调增加,且当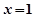 或
或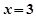 时,
时,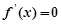
所以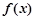 的极大值为
的极大值为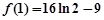 ,极小值为
,极小值为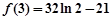 。。。。。。。6分
。。。。。。。6分
因为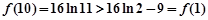
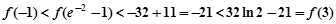
所以在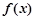 的三个单调区间
的三个单调区间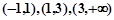 直线
直线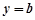 与
与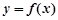 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当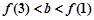 。。。。。。。7分
。。。。。。。7分
因此, 的取值范围为
的取值范围为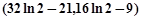 。。。。。。。。8分
。。。。。。。。8分
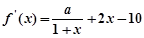 。。。。。。。1分
。。。。。。。1分所以
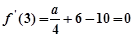 , 因此
, 因此 。。。。。。。2分
。。。。。。。2分(2)由(1)知,
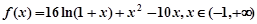
 。。。。。。。3分
。。。。。。。3分当
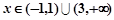 时,
时, 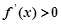
当
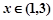 时,
时,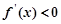 。。。。。。。4分
。。。。。。。4分所以
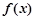 的单调增区间是
的单调增区间是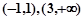
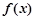 的单调减区间是
的单调减区间是 。。。。。。。5分
。。。。。。。5分(3)由(2)知,
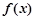 在
在 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在 上单调增加,且当
上单调增加,且当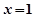 或
或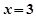 时,
时,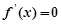
所以
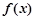 的极大值为
的极大值为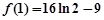 ,极小值为
,极小值为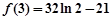 。。。。。。。6分
。。。。。。。6分因为
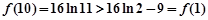
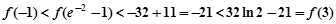
所以在
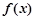 的三个单调区间
的三个单调区间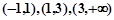 直线
直线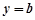 与
与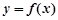 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当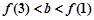 。。。。。。。7分
。。。。。。。7分因此,
 的取值范围为
的取值范围为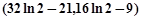 。。。。。。。。8分
。。。。。。。。8分本试题主要是考查了导数在研究函数中的运用。
(1)因为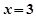 是函数
是函数 的一个极值点,那么可知在x=3处的到数值为零,得到参数a的值。
的一个极值点,那么可知在x=3处的到数值为零,得到参数a的值。
(2)由(1)知,
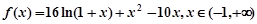
 从而求解函数的单调区间。
从而求解函数的单调区间。
(3)由(2)知,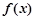 在
在 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在 上单调增加,且当
上单调增加,且当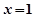 或
或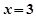 时,
时,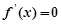
所以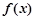 的极大值为
的极大值为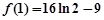 ,极小值为
,极小值为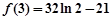 利用极值的符号确定参数的范围。
利用极值的符号确定参数的范围。
(1)因为
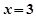 是函数
是函数 的一个极值点,那么可知在x=3处的到数值为零,得到参数a的值。
的一个极值点,那么可知在x=3处的到数值为零,得到参数a的值。(2)由(1)知,
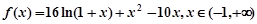
 从而求解函数的单调区间。
从而求解函数的单调区间。(3)由(2)知,
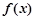 在
在 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在 上单调增加,且当
上单调增加,且当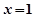 或
或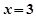 时,
时,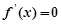
所以
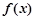 的极大值为
的极大值为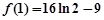 ,极小值为
,极小值为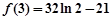 利用极值的符号确定参数的范围。
利用极值的符号确定参数的范围。
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
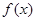 在R上满足f(x)=2f(4-x)-2x2+5x,则曲线
在R上满足f(x)=2f(4-x)-2x2+5x,则曲线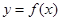 在点(2,f(2) )
在点(2,f(2) )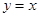
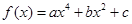 满足
满足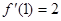 ,则
,则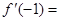 ( )
( )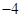
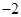
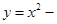 lnx上任意一点,则点P到直线y=x+3的最小距离为( )
lnx上任意一点,则点P到直线y=x+3的最小距离为( ) 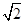
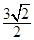
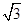
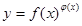 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得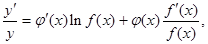 于是
于是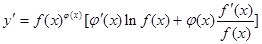 ,运用此方法可以求得函数
,运用此方法可以求得函数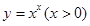 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________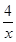 在点p(1,4)处的切线与直线l平行且距离为
在点p(1,4)处的切线与直线l平行且距离为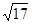 ,则直线l的方程为( )
,则直线l的方程为( )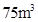 ,墙高为
,墙高为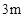 的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?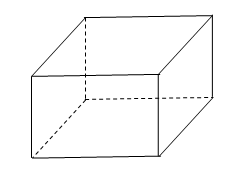
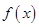 在
在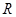 上的导函数为
上的导函数为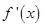 ,且
,且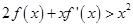 ,下面的不等式在
,下面的不等式在