题目内容
设函数f(x)=x3﹣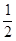 x2﹣2x﹣
x2﹣2x﹣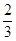 .
.
(1)求函数f(x)的单调递增、递减区间;
(2)当x∈[﹣1,1]时,f(x)<m恒成立,求实数m的取值范围.
(1)f(x)的单调增区间为(﹣∞,﹣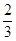 ]和[1,+∞),单调减区间为[﹣
]和[1,+∞),单调减区间为[﹣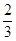 ,1]; (2)m>
,1]; (2)m>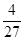 .
.
解析试题分析:(1)首先应求导数,利用导数的为正或为负,解对应不等式可得函数的单调增(减)区间;
(2)由不等式恒成立问题可通过分离参数等价转化成f(x)max<m,求函数f(x)的最大值即可.
试题解析:(1)f′(x)=3x2﹣x﹣2=0,得x=1,﹣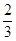 .
.
在(﹣∞,﹣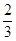 )和[1,+∞)上f′(x)>0,f(x)为增函数;
)和[1,+∞)上f′(x)>0,f(x)为增函数;
在(﹣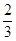 ,1)上f′(x)<0,f(x)为减函数.
,1)上f′(x)<0,f(x)为减函数.
所以所求f(x)的单调增区间为(﹣∞,﹣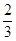 ]和[1,+∞),单调减区间为[﹣
]和[1,+∞),单调减区间为[﹣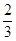 ,1].
,1].
(2)由(1)知,当x∈[﹣1,﹣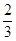 ]时,f′(x)>0,[﹣
]时,f′(x)>0,[﹣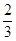 ,1]时,f′(x)<0
,1]时,f′(x)<0
∴f(x)≤f(﹣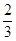 )=
)=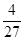 .
.
∵当x∈[﹣1,1]时,f(x)<m恒成立,
∴m>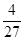 .
.
考点:1.利用导数研究函数的单调性;2.不等式的恒成立问题.

练习册系列答案
相关题目
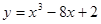
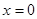 处的的切线方程;
处的的切线方程;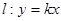 ,求切线方程.
,求切线方程.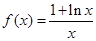 .
. 在区间
在区间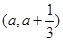
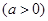 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围; 时,不等式
时,不等式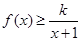 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;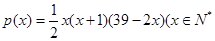 ,且
,且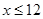 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
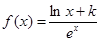 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线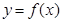 在点
在点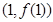 处的切线与x轴平行.
处的切线与x轴平行.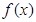 的单调区间;
的单调区间; 其中
其中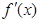 为
为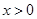 ,
,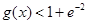 .
. ,
, (
( ).
). 的极值点,求
的极值点,求 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值; 在
在 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围. ,则
,则 展开式中的常数项为___________.
展开式中的常数项为___________.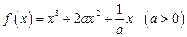 ,则
,则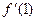 的最小值为
的最小值为 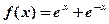 ,若曲线
,若曲线 上在点
上在点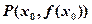 处的切线斜率为
处的切线斜率为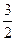
 ,则
,则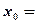 .
.