题目内容
设正四面体ABCD的四个面BCD，ACD，ABD，ABC的中心分别为O1，O2，O3，O4，则直线O1O2与O3O4所成角的大小为 .
以O1为原点，O1C为x轴，O1A为z轴，建立如图所示的坐标系，
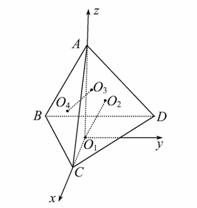
设AB＝1，则B(－
，－
，0)，D(－，，0)，C(
，0,0)，A(0,0，
)，∴O2(
，
，
)，O3(－
，0，)，O4(，－，)
∴
＝(，，)，
＝(，－
，0)，
∴·＝
－
＋0＝0，
∴O1O2⊥O3O4，即O1O2与O3O4所成的角为
.
答案：
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
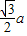；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d1，d2，d3，d4，则有d1+d2+d3+d4为定值 ．