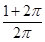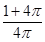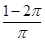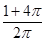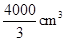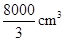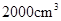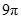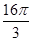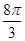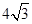题目内容
把正方形 沿对角线
沿对角线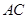 折起,当以
折起,当以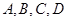 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线 和平面
和平面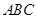 所成的角的大小为( )
所成的角的大小为( )
A.90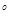 | B.30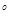 | C.60 | D.45 |
D
解析试题分析:当平面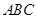 垂直于平面
垂直于平面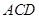 时,以
时,以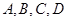 四点为顶点的三棱锥体积最大,此时找
四点为顶点的三棱锥体积最大,此时找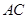 的重点
的重点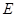 ,连接
,连接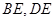 ,易证
,易证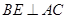 ,所以
,所以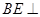 平面
平面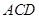 ,所以
,所以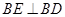 ,所以
,所以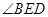 为直线
为直线 和平面
和平面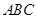 所成的角,所以
所成的角,所以
考点:本小题主要考查直线与平面所成角的求法,考查学生的空间想象能力.
点评:求直线与平面所成的角,关键是先作出角,再证明作出的角是要求的线面角,最后才是求角的大小.

练习册系列答案
相关题目
将边长为1的正方形ABCD,沿对角线AC折起,使BD=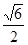 .则三棱锥D-ABC的体积为( )
.则三棱锥D-ABC的体积为( )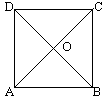
A.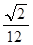 | B.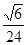 | C. | D.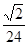 |
如图所示的直观图,其原来平面图形的面积是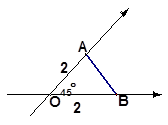
| A.4 |
B.4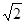 |
C.2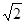 |
| D.8 |
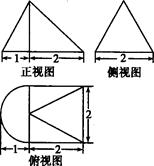
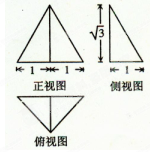
一个几何体的三视图如右图所示,则该几何体的体积为 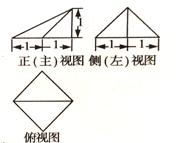
A.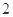 | B.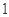 |
C.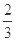 | D.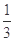 |