题目内容
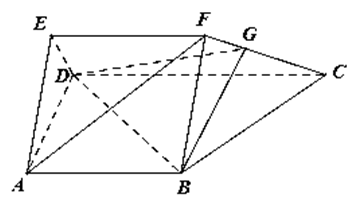
四棱锥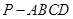 底面是平行四边形,面
底面是平行四边形,面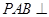 面
面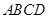 ,
, ,
,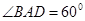 ,
, 分别为
分别为 的中点.
的中点.
(1)求证:
(2)求证: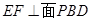
(3)求二面角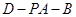 的余弦值.
的余弦值.
(1)见解析;(2)见解析;(3)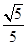 .
.
解析试题分析:(1)根据已有中点, , 推出
, 推出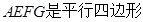 ,得到
,得到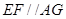 ,即得证;
,即得证;
(2)根据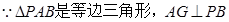 ,由余弦定理得出
,由余弦定理得出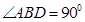
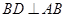 进一步得出根据
进一步得出根据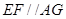 得证.
得证.
上述两小题,关键是要注意表述的规范性.
(3)解答本小题可利用“几何法”、“向量法”,应用“几何法”,要注意做好“作图,证明,计算”等工作.利用“向量法”,则要注意计算准确.
试题解析:(1) 1分
1分 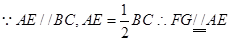
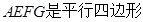 ,所以
,所以 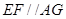 2分
2分  4分
4分 
(2)  ①
① 中,
中,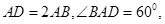 由余弦定理
由余弦定理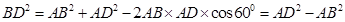 ,所以,
,所以,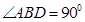 ,
,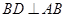 6分
6分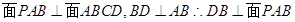
 ② 7分
② 7分
由 ①②可知,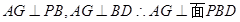
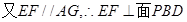 9分
9分 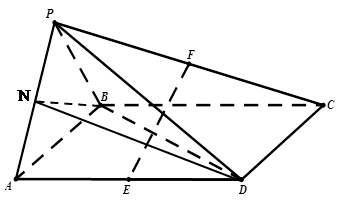
(3)取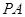 的中点
的中点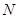 ,
,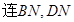
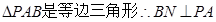
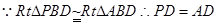
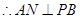
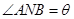 是二面角
是二面角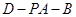
的平面角 11分
由(2)知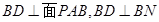
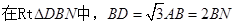
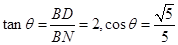 即二面角
即二面角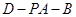 的余弦值为
的余弦值为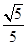 13分
13分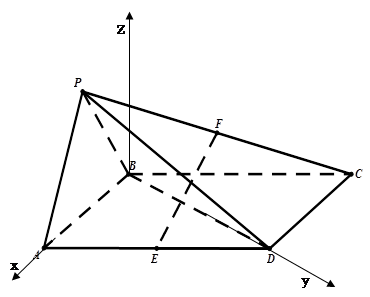
解法二 (1)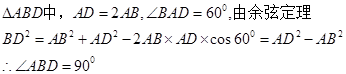 所以
所以 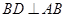
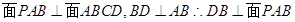
建系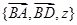 令
令 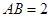
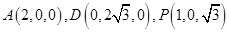 ,
,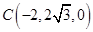
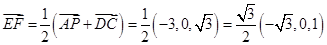
因为平面PAB的法向量 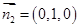
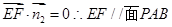
(2)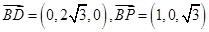
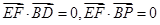
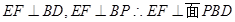
(3) 设平面PAD的法向量为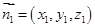
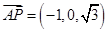 ,
,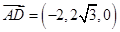
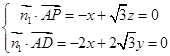 令
令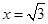 所以
所以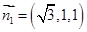
平面PAB的法向量 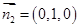
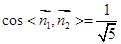 ,即二面角
,即二面角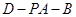 的余弦值为
的余弦值为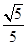
考点:平行关系,垂直关系,空间的角的计算.

练习册系列答案
相关题目
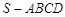 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面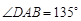 ,
, ,
,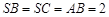 ,
,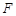 为线段
为线段 的中点.
的中点.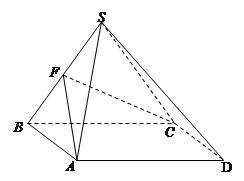
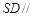 平面
平面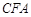 ;
;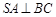 .
.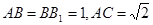 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
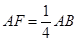
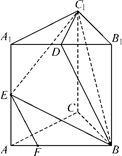
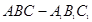 中,
中,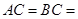
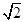 ,且
,且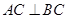 ,点
,点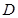 是
是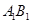 中点.
中点.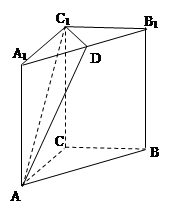
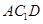 ⊥平面
⊥平面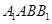 ;
;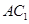 与平面
与平面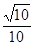 ,
,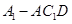 的体积.
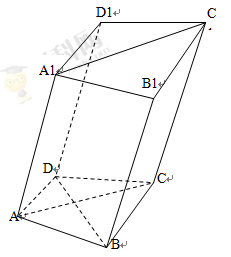
的体积.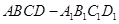 中,已知平面
中,已知平面 ,且
,且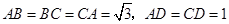 .
.
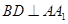 ;
;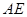 ∥平面
∥平面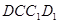 ,求
,求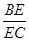 的值.
的值.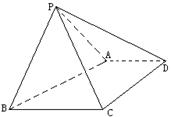
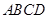 是梯形,
是梯形,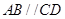 ,
,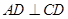 ,三角形
,三角形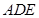 是等边三角形,且平面
是等边三角形,且平面 平面
平面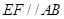 ,
,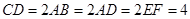 ,
,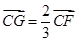
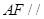 平面
平面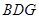 ;
;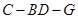 的余弦值.
的余弦值. 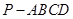 中,底面
中,底面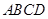 是矩形,
是矩形,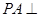 平面
平面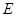 、
、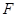 分别是
分别是 、
、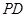 的中点.
的中点.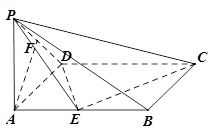
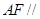 平面
平面 ;
; 与平面
与平面 所成角为
所成角为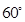 ,且
,且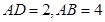 ,求点
,求点 到平面
到平面 的距离.
的距离.