题目内容
1.已知f(x)=(m-1)x2+3mx+3为偶函数,则f(x)在区间(-4,2)上为( )| A. | 增函数 | B. | 减函数 | C. | 先递增再递减 | D. | 先递减再递增 |
分析 由f(x)=(m-1)x2+3mx+3为偶函数,可得f(-x)=f(x)对任意的x都成立,代入可求m,结合二次函数的性质可求.
解答 解:因为f(x)=(m-1)x2+3mx+3为偶函数,所以f(-x)=f(x),
所以(m-1)x2-3mx+3=(m-1)x2+3mx+3,
即3m=0,所以m=0,
即f(x)=-x2+3,
由二次函数的性质可知,
f(x)=-x2+3在区间(-4,0)上单调递增,在(0,2)递减,
故选:C.
点评 本题主要考查了偶函数定义的应用,二次函数在闭区间上单调性及最值求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
12.2015年春晚过后,为了研究演员上春晚次数与受关注度的关系,某站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(Ⅰ)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\widehat{y}$=$\widehat{b}$+$\widehat{a}$,并就此分析:该演员上春晚12次时的粉丝数量;
(Ⅱ)若用$\frac{y_i}{x_i}(i=1,2,3,4,5)$表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.
(参考公式:$\widehat{y}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$)
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(Ⅱ)若用$\frac{y_i}{x_i}(i=1,2,3,4,5)$表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.
(参考公式:$\widehat{y}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$)
9.Sn是等差数列{an}的前n项和,如果S10=120,那么a3+a8的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
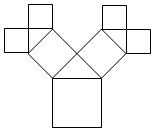 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.