Question

【题目】如图，四边形是边长为的正方形，平面平面， , ．

（Ⅰ）求证： 平面；

（Ⅱ）求三棱锥的体积．

Answer 1

【答案】（Ⅰ）证明见解析；（II）

【解析】试题分析：证明线面垂直，第一可利用线面垂直的判定定理，证明直线与平面内的两条相交直线垂直，进而说明线面垂直.求几何体的体积注意利用转化思想，包括顶点转化，底面转化，平行转化，对称转化、比例转化等，关键在于转化灵活.

试题解析：

（Ⅰ）平面平面，

平面平面， 平面ABEF, 且，

平面.

又因为平面， ．

又因为四边形为正方形， ．

平面BDE， ，

所以平面.

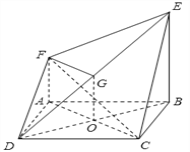
（Ⅱ）设 ，因为四边形为正方形，O是中点

设是中点，连接，则又

所以四边形是平行四边形

点C到平面DEF距离等于点A到平面DEF距离

所以体积为