题目内容
用诱导公式求下列三角函数值:(1)sin(-| 17π |
| 6 |
| 13π |
| 4 |
分析:(1)把所求式子的角度-
变为-4π+(π+
)后,利用诱导公式sin(2kπ+α)=sinα化简,再利用sin(π+α)=-sinα化简后,利用特殊角的三角函数值即可求出值;
(2)先根据余弦函数为偶函数把角度中的负号去掉,把
变为2π+(π+
),利用诱导公式cos(2kπ+α)=cosα化简,再利用cos(π+α)=-cosα化简后,利用特殊角的三角函数值即可求出值.
| 17π |
| 6 |
| π |
| 6 |
(2)先根据余弦函数为偶函数把角度中的负号去掉,把
| 13π |
| 4 |
| π |
| 4 |
解答:解:(1)sin(-
)=sin[-4π+(π+
)]
=sin(π+
)=-sin
=-
;
(2)cos(-
)=cos
=cos[2π+(π+
)]
=cos(π+
)=-cos
=-
.
| 17π |
| 6 |
| π |
| 6 |
=sin(π+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
(2)cos(-
| 13π |
| 4 |
| 13π |
| 4 |
| π |
| 4 |
=cos(π+
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
点评:此题考查了运用诱导公式化简求值,灵活变换角度,熟练掌握诱导公式是解题的关键.

练习册系列答案
相关题目
用诱导公式求下列三角函数值:
|
(1) |
(2)sin( -1574°); |
|
(3)sin( -2160°52′); |
(4)cos( -1751°36′); |
|
(5)cos1615°8′ ; |
(6) |
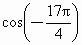
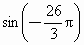
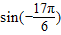 (2)
(2)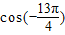 .
.