题目内容
已知双曲线C:2x2-y2=2与点P(1,2).(1)求过点P(1,2)的直线l的斜率k的取值范围,使l与C分别有一个交点,两个交点,没有交点.
(2)是否存在过P点的弦AB,使AB中点为P?
(3)若Q(1,1),试判断以Q为中点的弦是否存在?
解:(1)设直线l的方程为y-2=k(x-1),代入C的方程,并整理得(2-k2)x2+2(k2-2k)x-k2+4k-6=0,(*)
当k=±![]() 时,方程组有唯一解.
时,方程组有唯一解.
当k≠±![]() 时,由Δ=0,得k=
时,由Δ=0,得k=![]() .
.
所以当k=±![]() 或k=
或k=![]() 或k不存在时,l与C只有一个交点.
或k不存在时,l与C只有一个交点.
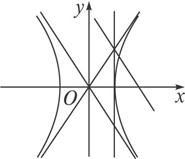
如图,当![]() <k<
<k<![]() 或k<-
或k<-![]() 或-
或-![]() <k<
<k<![]() 时,l与C有两个交点.
时,l与C有两个交点.
当k>![]() 时,l与C无交点.
时,l与C无交点.
(2)假设以P为中点的弦AB存在,
设A(x1,y1),B(x2,y2),
则x1、x2是方程(*)的两个根,
由韦达定理得![]() =1,
=1,
解得k=1.
所以这样的弦存在,方程为y=x+1.
(3)假设弦AB以Q为中点,且A(x1,y1),B(x2,y2),
所以2x12-y12=2,2x22-y22=2.
两式相减,得2(x1+x2)(x1-x2)=(y1+y2)(y1-y2),
所以2(x1-x2)=y1-y2.
所以AB的斜率为2,但渐近线斜率为±![]() ,结合图形知直线AB与C无交点.
,结合图形知直线AB与C无交点.
所以假设不正确,即以Q为中点的弦不存在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知双曲线C:2x2-y2=2与点P(1,2)
已知双曲线C:2x2-y2=2与点P(1,2)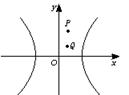
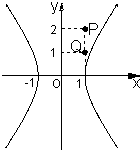 已知双曲线C:2x2-y2=2与点P(1,2)
已知双曲线C:2x2-y2=2与点P(1,2)