题目内容
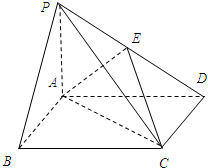 如图,P是平面ABCD外一点,四 边形ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,(1)求证平面PDC⊥平面PAD;
如图,P是平面ABCD外一点,四 边形ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,(1)求证平面PDC⊥平面PAD;(2)求二面角E-AC-D所成平面角的余弦值.
分析:(1)可利用PA⊥平面ABCD,证明CD⊥面PAD,从而可证面PDC⊥面PAD;
(2)设H为AD的中点,连EH,则EH∥PA,由PA⊥平面ABCD知EH⊥面ACD,过H作HO⊥AC于O,连EO则EO⊥AC,则∠EOH即为所求.
(2)设H为AD的中点,连EH,则EH∥PA,由PA⊥平面ABCD知EH⊥面ACD,过H作HO⊥AC于O,连EO则EO⊥AC,则∠EOH即为所求.
解答:证明:(1)∵四边形ABCD是矩形
∴CD⊥AD
∵PA⊥平面ABCD
∴CD⊥PA
∵AD与PA是相交直线
∴CD⊥面PAD
∵CD?面PAD
∴面PDC⊥面PAD
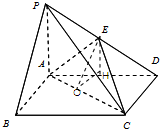
(2)设H为AD的中点,连EH,则EH∥PA,由PA⊥平面ABCD知EH⊥面ACD
过H作HO⊥AC于O,连EO则EO⊥AC∴∠EOH即为所求
在Rt△EHO中 而后OH=
∴OE=
∴∴cos∠EOH=
∴CD⊥AD
∵PA⊥平面ABCD
∴CD⊥PA
∵AD与PA是相交直线
∴CD⊥面PAD
∵CD?面PAD
∴面PDC⊥面PAD

(2)设H为AD的中点,连EH,则EH∥PA,由PA⊥平面ABCD知EH⊥面ACD
过H作HO⊥AC于O,连EO则EO⊥AC∴∠EOH即为所求
在Rt△EHO中 而后OH=
| 2 | ||
|
| 3 | ||
|
∴∴cos∠EOH=
| 2 |
| 3 |
点评:本题以线面垂直为载体,考查面面垂直,考查面面角,关键是正确运用面面垂直的判定定理.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目

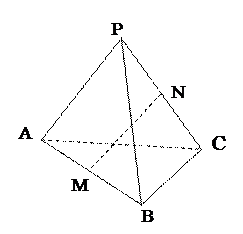

 (本小题满分12分)如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。
(本小题满分12分)如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。