题目内容
棱长为2的正方体ABCD-A1B1C1D1中，E为棱C1D1的中点，F为棱BC的中点，
（1）求证AE⊥DA1；
（2）求在线段AA1上找一点G，使AE⊥面DFG。
（1）求证AE⊥DA1；
（2）求在线段AA1上找一点G，使AE⊥面DFG。
解：（1）连接AD1，BC1，
由正方体的性质可知
，
又
，
∴
，
又AE
，
∴
；
（2）所求G点即为A1点，
证明如下：由（1） 知
，
取CD的中点H，连AH，EH，
由DF⊥AH，DF⊥EH，AH∩EH=H，
可证DF⊥平面AHE，
∴DF⊥AE，
又
，
∴
，
即AE⊥面DFG。
由正方体的性质可知
，又
，∴
，又AE
，∴
；（2）所求G点即为A1点，
证明如下：由（1） 知
，取CD的中点H，连AH，EH，
由DF⊥AH，DF⊥EH，AH∩EH=H，
可证DF⊥平面AHE，
∴DF⊥AE，
又
， ∴
，即AE⊥面DFG。
练习册系列答案
相关题目
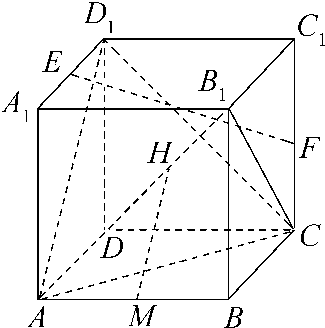如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F、M、H分别为A1D1、CC1、AB、DB1的中点．
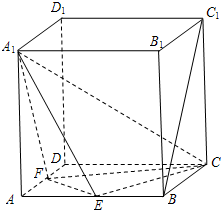（2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：