题目内容
不等式|x+ |-a+4>0对于一切非零实数x均成立,则实数a的取值范围是________.
|-a+4>0对于一切非零实数x均成立,则实数a的取值范围是________.
(-∞,6)
分析:由题意得|x+ |>a-4 对一切非零实数x均成立,由于|x+
|>a-4 对一切非零实数x均成立,由于|x+ |的最小值等于2,可得2>a-4,从而求得答案.
|的最小值等于2,可得2>a-4,从而求得答案.
解答:∵不等式|x+ |-a+4>0对于一切非零实数x均成立,∴|x+
|-a+4>0对于一切非零实数x均成立,∴|x+ |>a-4 对一切非零实数x均成立.
|>a-4 对一切非零实数x均成立.
由于|x+ |=|x|+
|=|x|+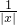 ≥2,故|x+
≥2,故|x+ |的最小值等于2,∴2>a-4,解得 a<6,
|的最小值等于2,∴2>a-4,解得 a<6,
故答案为 (-∞,6).
点评:本题考查查绝对值不等式的解法,基本不等式的应用以及函数的恒成立问题,求出|x+ |的最小值等于是解题的关键.
|的最小值等于是解题的关键.
分析:由题意得|x+
 |>a-4 对一切非零实数x均成立,由于|x+
|>a-4 对一切非零实数x均成立,由于|x+ |的最小值等于2,可得2>a-4,从而求得答案.
|的最小值等于2,可得2>a-4,从而求得答案.解答:∵不等式|x+
 |-a+4>0对于一切非零实数x均成立,∴|x+
|-a+4>0对于一切非零实数x均成立,∴|x+ |>a-4 对一切非零实数x均成立.
|>a-4 对一切非零实数x均成立.由于|x+
 |=|x|+
|=|x|+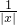 ≥2,故|x+
≥2,故|x+ |的最小值等于2,∴2>a-4,解得 a<6,
|的最小值等于2,∴2>a-4,解得 a<6,故答案为 (-∞,6).
点评:本题考查查绝对值不等式的解法,基本不等式的应用以及函数的恒成立问题,求出|x+
 |的最小值等于是解题的关键.
|的最小值等于是解题的关键. 
练习册系列答案
相关题目
不等式
≤0的解集为{x|-1<x≤0或x=2},则点(a,b+c)在( )
| (x-a)2(x+b) |
| x-c |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |