题目内容
17.设命题p:函数y=f(x)不是偶函数,命题q:函数y=f(x)是单调函数,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 由q⇒p,反之不成立.例如取f(x)=(x-1)2不是偶函数,但是此函数在R上不单调.
解答 解:命题p:函数y=f(x)不是偶函数,命题q:函数y=f(x)是单调函数,
则q⇒p,反之不成立.例如f(x)=(x-1)2不是偶函数,但是此函数在R上不单调.
则p是q的必要不充分条件.
故选:B.
点评 本题考查了函数的奇偶性单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
12.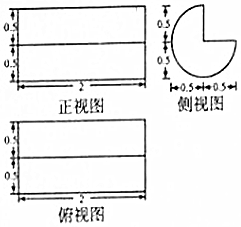 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )| A. | 94.20元 | B. | 240.00元 | C. | 282.60元 | D. | 376.80元 |
2.已知函数f(x)=|2x-2|+b的两个零点分别为x1,x2(x1>x2),则下列结论正确的是( )
| A. | 1<x1<2,x1+x2<2 | B. | 1<x1<2,x1+x2<1 | C. | x1>1,x1+x2<2 | D. | x1>1,x1+x2<1 |
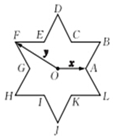 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.