Question

（2012•合肥一模）若函数f（x）=|sinx|的图象与直线y=kx（k＞0）仅有三个公共点，且其横坐标分别为α，β，γ（α＜β＜γ），给出下列结论：
①k=-cosγ；②γ∈（0，π）；③γ=tanγ；④sin2γ=

2γ

1+γ2

其中正确的是

①③④

（填上所有正确的序号）

Answer 1

分析：可作出函数f（x）=|sinx|与直线y=kx（k＞0）仅有三个公共点的图象，利用导数与斜率的坐标公式可分别求得k，进一步分析即可得到答案．

解答：解：函数f（x）=|sinx|的图象与直线y=kx（k＞0）仅有三个公共点，其图象如下：

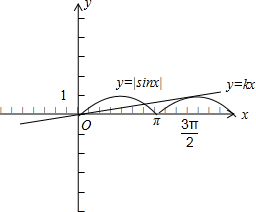
由图可知，α=0，

π

2

＜β＜π＜γ＜

3π

2

，可排除②
当π＜x＜

3π

2

，
f（x）=|sinx|=-sinx，
∵直线y=kx（k＞0）与 y=-sinx 相切，
∴k=

-sinγ

γ

，同时，由 y′=-cosx，
∴k=-cosγ，故①正确；
∴-

sinγ

γ

=-cosγ，所以 γ=tanγ，故③正确；
∴由万能公式可得sin2γ=

2tanγ

1+tan2γ

=

2γ

1+γ2

，故④正确．
故答案为：①③④．

点评：本题考查函数的零点与方程根的关系，考查正弦函数的图象，考查导数的几何意义与万能公式，属于难题．