题目内容
18.将函数y=cos2x的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=f(x)•sin x的图象,则f(x)的表达式可以是( )| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数y=cos2x的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=cos2(x-$\frac{π}{4}$)=sin2x的图象,
再根据所得函数的解析式为 y=f(x)•sinx,故f(x)=2cosx,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
9.已知点P(-1,3,-4),且该点在三个坐标平面yOz平面,zOx平面、xOy平面上的射影的坐标依次为A、B、C,则以PA、PB、PC为棱的平行六面体体积为( )
| A. | 12 | B. | 6 | C. | 4 | D. | 以上结论都不对 |
7.如图所示,程序框图输出的结果为( )
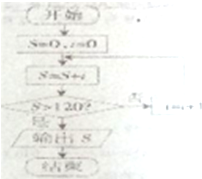

| A. | 15 | B. | 16 | C. | 136 | D. | 153 |