题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为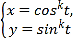
![]() 为参数
为参数![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
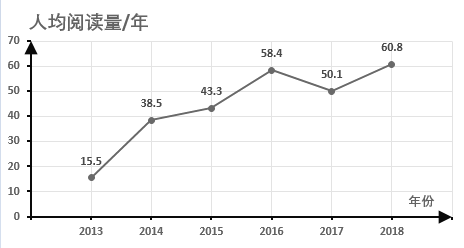
(1)当![]() 时,
时,![]() 是什么曲线?
是什么曲线?
(2)当![]() 时,求
时,求![]() 与
与![]() 的公共点的直角坐标.
的公共点的直角坐标.
【答案】(1)曲线![]() 表示以坐标原点为圆心,半径为1的圆;(2)
表示以坐标原点为圆心,半径为1的圆;(2)![]() .
.
【解析】
(1)利用![]() 消去参数
消去参数![]() ,求出曲线
,求出曲线![]() 的普通方程,即可得出结论;
的普通方程,即可得出结论;
(2)当![]() 时,
时,![]() ,曲线
,曲线![]() 的参数方程化为
的参数方程化为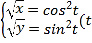 为参数),两式相加消去参数
为参数),两式相加消去参数![]() ,得
,得![]() 普通方程,由
普通方程,由![]() ,将曲线
,将曲线![]() 化为直角坐标方程,联立
化为直角坐标方程,联立![]() 方程,即可求解.
方程,即可求解.
(1)当![]() 时,曲线
时,曲线![]() 的参数方程为
的参数方程为![]() 为参数),
为参数),
两式平方相加得![]() ,
,
所以曲线![]() 表示以坐标原点为圆心,半径为1的圆;
表示以坐标原点为圆心,半径为1的圆;
(2)当![]() 时,曲线
时,曲线![]() 的参数方程为
的参数方程为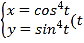 为参数),
为参数),
所以![]() ,曲线
,曲线![]() 的参数方程化为
的参数方程化为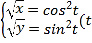 为参数),
为参数),
两式相加得曲线![]() 方程为
方程为![]() ,
,
得![]() ,平方得
,平方得![]() ,
,
曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
曲线![]() 直角坐标方程为
直角坐标方程为![]() ,
,
联立![]() 方程
方程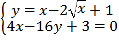 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
![]() ,
,![]() 公共点的直角坐标为
公共点的直角坐标为![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目