题目内容
(本小题满分13分)
已知双曲线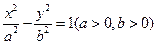 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与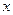 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又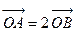 ,
,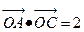 过点F的直线与双曲线右交于点M、N,点P为点M关于
过点F的直线与双曲线右交于点M、N,点P为点M关于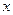 轴的对称点。
轴的对称点。
(1)求双曲线的方程;
(2)证明:B、P、N三点共线;
(3)求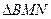 面积的最小值。
面积的最小值。
已知双曲线
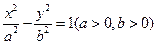 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与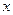 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又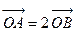 ,
,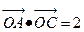 过点F的直线与双曲线右交于点M、N,点P为点M关于
过点F的直线与双曲线右交于点M、N,点P为点M关于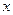 轴的对称点。
轴的对称点。(1)求双曲线的方程;
(2)证明:B、P、N三点共线;
(3)求
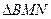 面积的最小值。
面积的最小值。解:(1)易得双曲线方程为
(2)由(1)可知得点 设直线L的方程为:
设直线L的方程为:
由: 可得
可得
设
所以 所以
所以
因为
=
=
=0
所以向量 共线。所以B, P,N三点共线
共线。所以B, P,N三点共线
(3)因为 直线L与双曲线右支相交于M,N
所以 所以
所以

令

由
当 时,三角形BMN面积的最小值为18
时,三角形BMN面积的最小值为18

(2)由(1)可知得点
 设直线L的方程为:
设直线L的方程为:
由:
 可得
可得
设

所以
 所以
所以
因为

=

=

=0
所以向量
 共线。所以B, P,N三点共线
共线。所以B, P,N三点共线(3)因为 直线L与双曲线右支相交于M,N
所以
 所以
所以

令


由

当
 时,三角形BMN面积的最小值为18
时,三角形BMN面积的最小值为18略

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
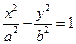 的左、右焦点分别F1、F2,O为双曲线的中心,P是双曲线右支上的点,
的左、右焦点分别F1、F2,O为双曲线的中心,P是双曲线右支上的点,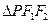 的内切圆的圆心为I,且⊙I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的率心率,则 ( )
的内切圆的圆心为I,且⊙I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的率心率,则 ( )
 、
、 为双曲线C:
为双曲线C: 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠

 ,则
,则 ( )
( ) 2
2
 作与直径垂直的直线分别与圆周交
作与直径垂直的直线分别与圆周交 ,如果以
,如果以



 ,其中正数a、b的等差中项是
,其中正数a、b的等差中项是 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线的离心率为
则双曲线的离心率为 



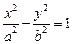 (a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
(a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为  ,则以C的右焦点为圆心,且与双曲线C的渐
,则以C的右焦点为圆心,且与双曲线C的渐 近线相切的圆的方程是
近线相切的圆的方程是  是由双曲线
是由双曲线 的两条渐近线和直线
的两条渐近线和直线 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当 时,
时, 的最大值为( )
的最大值为( )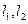 ,经
,经 过右焦点F垂直
过右焦点F垂直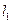 的直线分别交
的直线分别交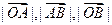 成等差数列,且
成等差数列,且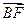 与
与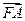 同向,则双曲线的离心率 .
同向,则双曲线的离心率 .