题目内容

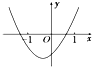已知f（x）=（x-a）（x-b）（其中b＜a），若f（x）的图象如图所示，则函数g（x）=a^x+b的图象是（　　）

A、

B、

C、

D、

分析：根据f（x）的图象可得b＜-1，且0＜a＜1，函数g（x）=a^x+b是减函数，且图象与y轴的交点（0，-b）在y轴的负半轴上，结合所给的选项，可得结论．

解答：解：根据f（x）=（x-a）（x-b）（其中b＜a）的图象可得b＜-1，且0＜a＜1，
故函数g（x）=a^x+b是减函数，且图象与y轴的交点（0，-b）在y轴的负半轴上，
结合所给的选项，
故选A．

点评：本题主要考查二次函数的图象和性质，函数的单调性和特殊点，属于基础题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知f （x）=sin （x+

），g （x）=cos （x-

），则下列命题中正确的是（　　）

A、函数y=f（x）•g（x）的最小正周期为2π

B、函数y=f（x）•g（x）是偶函数

C、函数y=f（x）+g（x）的最小值为-1

D、函数y=f（x）+g（x）的一个单调增区间是[-

已知f（x）=

．
（1）当1≤x＜2时，求g（x）；
（2）当x∈R时，求g（x）的解析式，并画出其图象；
（3）求方程x^f[g（x）]=2g[f（x）]的解．

已知f （x）=2sin（x+

．
（1）化简f （x）的解析式；
（2）若0≤θ≤π，求θ使函数f （x）为偶函数；
（3）在（2）成立的条件下，求满足f （x）=1，x∈[-π，π]的x的集合．

已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x²-kx³．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
（Ⅲ）若 $数学公式$ ，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间 $数学公式$ 上的值域为 $数学公式$ ，若存在，求出a的值；若不存在，请说明理由．

已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x²-kx³．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
（Ⅲ）若

，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间

上的值域为

，若存在，求出a的值；若不存在，请说明理由．