题目内容
已知函数

(1) 时,求函数
时,求函数 定义域;
定义域;
(2)当 时,函数
时,函数 有意义,求实数
有意义,求实数 的取值范围;
的取值范围;
(3) 时,函数
时,函数 的图像与
的图像与
 无交点,求实数
无交点,求实数 的取值范围.
的取值范围.
(1) 的定义域为
的定义域为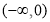 ;(2)
;(2) ;(3)
;(3) 或
或 .
.
【解析】(1)对数型函数有意义,须使真数大于 即:
即: ,得到函数的定义域;(2)恒成立问题一般都是求最值,本题利用分离变量得到
,得到函数的定义域;(2)恒成立问题一般都是求最值,本题利用分离变量得到 且
且 ,换元变形,进一步用单调性法求范围;(3)关于交点个数问题,分离变量,分别求出两个函数的值域,根据题意得到结果.
,换元变形,进一步用单调性法求范围;(3)关于交点个数问题,分离变量,分别求出两个函数的值域,根据题意得到结果.
试题分析:
试题解析:(1) 时,
时,
 ,定义域为
,定义域为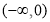 . 3分
. 3分
(2)由题 对一切
对一切 恒成立.
恒成立.
 令
令
 在
在 上单减,在
上单减,在 上单增.
上单增.

 . 8分
. 8分
(3) 时,
时,
 ,记
,记
令 ,
, 在
在 上单调递减.
上单调递减.

 ,
,
 ,
,
 图像无交点,
图像无交点,
 或
或 . 14分
. 14分
考点:1.偶函数的性质;2.换元法求函数求值;3.对数函数求最值.

练习册系列答案
相关题目
 的图像可能是( ) .
的图像可能是( ) .



 中,角
中,角 对应的边分别为
对应的边分别为 .若
.若 则“
则“ ”是“
”是“ ”的
”的 满足
满足 ,则称为满足“倒负”变换的函数,下列函数:
,则称为满足“倒负”变换的函数,下列函数: ;②
;② ;③
;③ 其中满足“倒负”变换的函数是 ( )
其中满足“倒负”变换的函数是 ( ) 的图象是下面图中的( )
的图象是下面图中的( )



 ,
, ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. ,若函数
,若函数 ,则
,则 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 上,并且经过圆
上,并且经过圆 与圆
与圆





 交点的圆的方程为 .
交点的圆的方程为 . 的解集为A,
的解集为A, 的解集为B,
的解集为B, 的解集为C,若
的解集为C,若 ,求
,求 的值
的值