Question

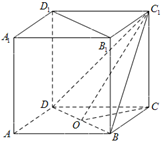如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点O是BD中点．
（Ⅰ） 求证：平面BDD₁B₁⊥平面C₁OC；
（Ⅱ） 求二面角C₁-BD-C的正切值．

Answer 1

分析：（Ⅰ）利用线面垂直的判定定理证明线面垂直，再利用面面垂直的判定定理证明平面BDD₁B₁⊥平面C₁OC；
（Ⅱ）由（Ⅰ）可知∠C₁OC是二面角C₁-BD-C的平面角，在Rt△C₁OC中，求二面角C₁-BD-C的正切值．

解答：（Ⅰ）证明：在正方体ABCD-A₁B₁C₁D₁中，点O是BD中点，
∵BC₁=DC₁，BC=DC，
∴C₁O⊥BD，CO⊥BD-------------------（2分）
∵C₁O∩CO=O，C₁O?平面C₁OC，CO?平面C₁OC，
∴BD⊥平面C₁OC------------------（5分）
∵BD?平面BDD₁B₁，∴平面BDD₁B₁⊥平面C₁OC．--------------（7分）
（Ⅱ）由（Ⅰ）可知∠C₁OC是二面角C₁-BD-C的平面角---------------（11分）
则

C

1

C=1，OC=

2

2

∴在Rt△C₁OC中，tan∠C1OC=

C1C

OC

=

2

故二面角C₁-BD-C的正切值为

2

．---------------（14分）

点评：本题考查面面垂直，考查面面角，解题的关键是利用线面垂直的判定定理证明线面垂直．