题目内容
12．
如图，在Rt△ABC中，∠B=30°，∠C=60°，AC=a，动点P，Q同时从A出发，沿周界运动，点P沿A→B→C；动点Q沿A→C→B运动到相遇时停止，它们的速度之比是1：3，点P走过的路程为x，△APQ的面积为y，写出y关于x的函数解析式，并求出定义域．
分析 先根据点Q的位置进行分类讨论，然后分别求出三角形的面积，从而可得函数f（x）的解析式，定义域．
解答 解：因为AP=x，动点Q的速度是动点P的运动速度的3倍，
所以AQ=3x，当点Q在线段AC上时，0＜x≤$\frac{1}{3}$时，三角形APQ为直角三角形，S=$\frac{1}{2}$x•3x=$\frac{3}{2}$x2；
当点Q在线段CB上时，$\frac{1}{3}$＜x≤1时，作出示意图如下：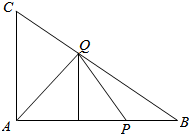
△APQ的高为 $\frac{BQ}{BC}$×AC=$\frac{3-2x}{2}$$\frac{3-2x}{2}$×1=$\frac{3-2x}{3}$，
所以S=$\frac{1}{2}$x•$\frac{3-2x}{2}$=$\frac{3x-{3x}^{2}}{4}$；
当Q在线段AB上时，不能构成三角形，
所以函数f（x）=$\left\{\begin{array}{l}{{\frac{3}{2}x}^{2}，（0＜x≤\frac{1}{3}）}\\{\frac{3x-{3x}^{2}}{4}，（\frac{1}{3}＜x≤1）}\end{array}\right.$．
函数的定义域是：（0，1]．
点评 本题主要考查了分段函数的应用，同时考查了学生分析问题和解决问题的能力，以及运算求解的能力．
练习册系列答案
相关题目
极坐标方程ρ=$\frac{ep}{1-ecosθ}$，（p＞0，e＞0），可以转化为平面直角坐标方程$\frac{{\sqrt{{x^2}+{y^2}}}}{{|{x+p}|}}$=e，该式子可以解释为：点（x，y）到原点的距离与到x=-p的距离之比为e，根据圆锥曲线的定义可以得到：ρ=$\frac{ep}{1-ecosθ}$表示一个以原点为其中一个焦点，以x=-p为对应准线的圆锥曲线．如图：过椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的左焦点C作CP1，CP2，CP3…CP10等分∠ACB（A，B分别为椭圆的左右顶点），记P1，P2，P3…P10到左准线的距离分别为d1，d2，d3…d10，则$\frac{1}{d_1}$+$\frac{1}{d_2}$+$\frac{1}{d_3}$+…+$\frac{1}{{{d_{10}}}}$=$\frac{{10\sqrt{7}}}{9}$．