题目内容
正态总体的概率密度函数为f(x)=| 1 | ||
|
| (x-3)2 |
| 50 |
分析:根据正态总体的概率密度函数,可以知道x-μ=x-3,μ是随机变量取值的平均水平的特征数,也就是这组数据的样本均值,正态密度曲线是关于x=μ对称的,本函数的曲线关于x=3对称,根据对称性得到结果.
解答:解:∵正态总体的概率密度函数为f(x)=
e-
,
∴根据密度函数可以知道x-μ=x-3,
μ是随机变量取值的平均水平的特征数,也就是这组数据的样本均值,
正态密度曲线是关于x=μ对称的,
∴本函数的曲线关于x=3对称,
∴P(x<3)=
,
故答案为:
| 1 | ||
|
| (x-3)2 |
| 50 |
∴根据密度函数可以知道x-μ=x-3,
μ是随机变量取值的平均水平的特征数,也就是这组数据的样本均值,
正态密度曲线是关于x=μ对称的,
∴本函数的曲线关于x=3对称,
∴P(x<3)=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查正态密度曲线的结构特点,要求从函数上看出密度曲线的变化特点,结合正态分布曲线的性质来解题,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正态总体的概率密度函数为f(x)=
e-
(x∈R),则总体的平均数和标准差分别是( )
| 1 | ||
|
| x2 |
| 8 |
| A、0和8 | B、0和4 |
| C、0和3 | D、0和2 |
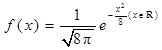 ,则总体的平均数
,则总体的平均数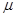 和标准差
和标准差 分别为( )
分别为( ) ,则总体的平均数和标准差分别是
,则总体的平均数和标准差分别是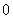 和
和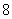 B.
B.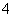 C.
C.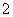 D.
D.