题目内容
【题目】某学校有n个班(n为给定正整数),且每班的男生与女生人数至多相差1.现该学校进行乒乓球比赛,规则如下:同一班的选手之间不比赛,不同班的每两名选手都比赛一场.我们称在同性别选手间的比赛为同打,异性别选手间的比赛为异打.若同打场数与异打场数至多相差1,求有奇数名学生的班级至多有多少个?
【答案】见解析
【解析】
设有奇数名学生的班最多有m个,![]() ,k为正整数,r为非负整数且
,k为正整数,r为非负整数且![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() :
:
当![]() 且
且![]() 时,
时,![]() .
.
记这n个班为![]() ,且
,且![]() 班有
班有![]() 个男生,
个男生,![]() 个女生,并设
个女生,并设![]() ,
,![]() .
.
则![]() 且m为
且m为![]() 中不为0的个数,这里
中不为0的个数,这里![]() 班有奇数名学生即
班有奇数名学生即![]() .
.
于是,同打场数为![]() ,异打场数为
,异打场数为![]() .
.
由题意知![]()
![]() 或
或![]() .
.
若![]() ,则不考虑
,则不考虑![]() 班,此时对结论无影响(此班学生数为偶数).
班,此时对结论无影响(此班学生数为偶数).
于是由m的性质知最后恰有m个![]() 不为0不妨设
不为0不妨设![]() 班学生数为奇数.故只要在
班学生数为奇数.故只要在![]() 及
及![]() 或
或![]() 的条件下,求m所能取到的最大值.
的条件下,求m所能取到的最大值.
设有x个![]() 为1,y个
为1,y个![]() 为
为![]() .则
.则![]() 且
且![]() 或
或![]() ,这里
,这里![]() .
.
当![]() 时,由m或
时,由m或![]() 或
或![]() 为平方数知
为平方数知![]() ,故
,故![]() .令
.令![]() ,
,![]() 时,
时,![]() ,故此时所求m为
,故此时所求m为![]() .
.
当![]() 时,由
时,由![]() 及令
及令![]() ,
,![]() 时,
时,![]() ,知此时所求m为n.
,知此时所求m为n.
同理![]() ,
,![]() 时有
时有![]() .
.
当![]() 且
且![]() 时,由m或
时,由m或![]() 或
或![]() 为完全平方数知:
为完全平方数知:
若m为平方数,则![]() 为最大值:若
为最大值:若![]() 为平方数,则
为平方数,则![]() 为最大值;若
为最大值;若![]() 为平方数,则
为平方数,则![]() 为最大值.
为最大值.
由m的性质知,![]() ,令
,令![]() ,其余的为
,其余的为![]() 时取到.
时取到.
综上即得结论.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某同学为研究“网络游戏对当代青少年的影响”作了一次调查,共调查了50名同学,其中男生26人,有8人不喜欢玩游戏,而调查的女生中有9人喜欢玩游戏.
(1)根据以上数据完成2×2的列联表;
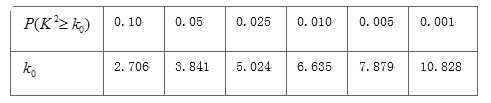
(2)根据以上数据,在犯错误的概率不超过0.025的前提下,能否认为“喜欢玩电脑游戏与性别有关系”?
男生 | 女生 | 总计 | |
喜欢玩游戏 | |||
不喜欢玩游戏 | |||
总计 |

| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |