题目内容
已知向量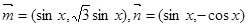 ,设函数
,设函数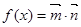 .
.
(1)求函数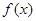 在
在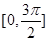 上的单调递增区间;
上的单调递增区间;
(2)在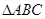 中,
中,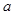 ,
,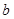 ,
,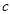 分别是角
分别是角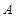 ,
,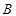 ,
,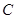 的对边,
的对边,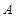 为锐角,若
为锐角,若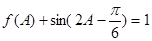 ,
,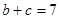 ,
,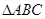 的面积为
的面积为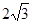 ,求边
,求边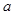 的长.
的长.
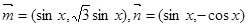 ,设函数
,设函数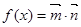 .
.(1)求函数
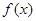 在
在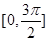 上的单调递增区间;
上的单调递增区间;(2)在
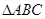 中,
中,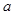 ,
,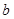 ,
,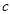 分别是角
分别是角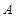 ,
,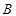 ,
,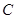 的对边,
的对边,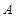 为锐角,若
为锐角,若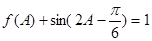 ,
,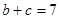 ,
,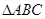 的面积为
的面积为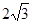 ,求边
,求边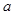 的长.
的长.(1)函数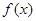 在
在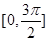 上的单调递增区间为
上的单调递增区间为 ,
, ;(2)边
;(2)边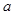 的长为
的长为 .
.
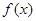 在
在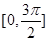 上的单调递增区间为
上的单调递增区间为 ,
, ;(2)边
;(2)边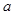 的长为
的长为 .
. 试题分析:(1)根据平面向量的数量积,应用和差倍半的三角函数公式,将
 化简为
化简为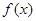
 .通过研究
.通过研究
的单调减区间得到函数
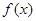 在
在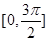 上的单调递增区间为
上的单调递增区间为 ,
, .
.(2)根据两角和的正弦公式,求得
 ,
,利用三角形的面积,解得
 ,
,结合
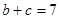 ,由余弦定理得
,由余弦定理得
从而得解.
试题解析:(1)由题意得

 3分
3分令
 ,
,
解得:
 ,
,
 ,
, ,或
,或
所以函数
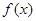 在
在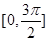 上的单调递增区间为
上的单调递增区间为 ,
, 6分
6分(2)由
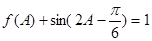 得:
得:
化简得:

又因为
 ,解得:
,解得: 9分
9分由题意知:
 ,解得
,解得 ,
,又
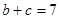 ,所以
,所以

故所求边
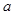 的长为
的长为 . 12分
. 12分
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ,
, ,函数
,函数 ,
,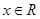 .
.
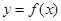 的图像的对称中心坐标;
的图像的对称中心坐标; 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 上的图像.
上的图像. sinxcosx-2cos2x+l.
sinxcosx-2cos2x+l.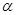 ∈(0,
∈(0, ),且f(
),且f(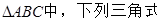 ①sin(A+B)+sinC;②cos(B+C)+cosA;③
①sin(A+B)+sinC;②cos(B+C)+cosA;③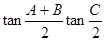
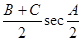 ,其中恒为定值的是 ( )
,其中恒为定值的是 ( ) sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)=
sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)= ,且当x∈[0,
,且当x∈[0, ]时,f(x)的最大值为1.
]时,f(x)的最大值为1. 有实根,则实数
有实根,则实数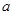 的取值范围为
的取值范围为 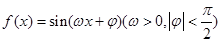 的最小正周期为
的最小正周期为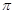 ,若其图象向右平移
,若其图象向右平移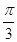 个单位后关于y轴对称,则( )
个单位后关于y轴对称,则( )



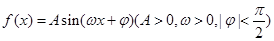 的部分图像如图示,则将
的部分图像如图示,则将 的图像向右平移
的图像向右平移 个单位后,得到的图像解析式为( )
个单位后,得到的图像解析式为( )




 中,已知
中,已知 ,那么
,那么