题目内容
如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2。

(1)求证:A1C1与AC共面,B1D1与BD共面;
(2)求证:平面A1ACC1⊥平面B1BDD1;
(3)求二面角A-BB1-C的大小(用反三角函数值圾示)。
(2)求证:平面A1ACC1⊥平面B1BDD1;
(3)求二面角A-BB1-C的大小(用反三角函数值圾示)。
解:(1)∵ 平面 平面 , , 平面 平面 ∴  , , ,平面 ,平面 平面 平面 于是  , , 设  分别为 分别为 的中点,连结 的中点,连结 , ,有  ∴  , ,于是  由  ,得 ,得 , ,故  , , 与 与 共面 共面过点  作 作 平面于点 平面于点 , ,则  ,连结 ,连结 , ,于是  , , , ,∴  ∵  , ,∴  ∵  , ,∴  所以点O在BD上,故  与 与 共面。 共面。(2)证明:∵  平面 平面 , ,∴  , ,又  (正方形的对角线互相垂直), (正方形的对角线互相垂直), 与 与 是平面 是平面 内的两条相交直线, 内的两条相交直线,∴  平面 平面 又平面  过 过 , ,∴平面  平面 平面 。 。(3)解:∵直线DB是直线  在平面 在平面 上的射影, 上的射影, , ,根据三垂线定理,有  过点A在平面  内作 内作 于M,连结 于M,连结 , ,则  平面 平面 , ,于是  , ,所以,  是二面角 是二面角 的一个平面角 的一个平面角根据勾股定理,有  ∵  ,有 ,有 , , , , , ,  , , , ,二面角  的大小为 的大小为 |
 |

练习册系列答案
相关题目
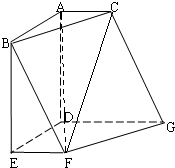 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.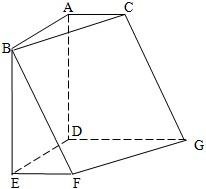 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG,且AC=EF=1,AB=AD=DE=DG=2.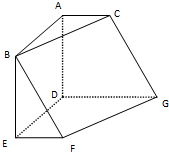 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,ED⊥DG,EF∥DG.且AC=EF=1,AB=AD=DE=DG=2.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,ED⊥DG,EF∥DG.且AC=EF=1,AB=AD=DE=DG=2.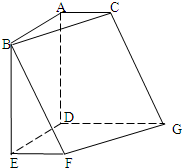 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.