题目内容
已知 ,
, ,函数
,函数 ,
, .
.
(1)求函数 的零点的集合;
的零点的集合;
(2)求函数 的最小正周期及其单调增区间.
的最小正周期及其单调增区间.
(1)函数 的零点的集合是
的零点的集合是 ;
;
(2)函数 的最小正周期为
的最小正周期为 ,单调递增区间为
,单调递增区间为 .
.
解析试题分析:(1)先将函数 求出来并化简,然后令
求出来并化简,然后令 ,解此方程即可得到函数
,解此方程即可得到函数 的零点的集合;(2)利用向量的数量积的定义将函数
的零点的集合;(2)利用向量的数量积的定义将函数 的解析式化简为
的解析式化简为 ,利用公式
,利用公式 求出函数
求出函数 的最小正周期,然后将
的最小正周期,然后将 视为一个整体,解不等式
视为一个整体,解不等式
 即可得到函数
即可得到函数 的单调递增区间.
的单调递增区间.
试题解析:(1) ,
, ,
,
令 ,
, ,解得
,解得 ,
,
故函数 的零点的集合是
的零点的集合是 ;
;
(2) ,
, ,
, ,
, ,即函数
,即函数 的最小正周期为
的最小正周期为 ,
,
由 ,解得
,解得 ,
,
故函数 的单调递增区间为
的单调递增区间为 .
.
考点:1.平面向量的数量积;2.函数的零点;3.三角函数的周期性;4.三角函数的单调性

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,且
,且 与夹角为
与夹角为 ,求
,求 ;
; 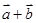 的夹角
的夹角 ,求
,求 的值。
的值。 ,
, ,已知函数
,已知函数 在
在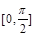 上的最大值为6.
上的最大值为6. 的值;
的值; ,
, .求
.求 的值.
的值. .
. 三点共线,求实数
三点共线,求实数 的值;
的值; 成立
成立 ,
, ,-
,- <θ<
<θ< ,求θ;
,求θ; 的最大值.
的最大值. =
= ,
,  =
=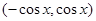 ,
,  =
=
 ,求向量
,求向量 时,求函数
时,求函数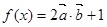 的最大值
的最大值 ,且
,且 与
与 的夹角为120°.
的夹角为120°. ; (2)
; (2)  ; (3)
; (3)  .
. 、
、 、
、
 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ,且
,且 ,求
,求 且
且 与
与 垂直,求
垂直,求 .
.