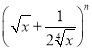题目内容
【题目】关于
的方程
，给出下列四个命题
①存在实数
，使得方程恰有2个不同的实根；
②存在实数，使得方程恰有4个不同的实根；
③存在实数，使得方程恰有5个不同的实根；
④存在实数，使得方程恰有7个不同的实根
A.3B.2C.1D.0
【答案】A
【解析】
将方程根的问题转化成函数图象问题，画出函数图象，结合图象可得结论。
令
，关于
的方程
，
可化为
①，
，对称轴为
。
（1）当
，即
时，方程①无解，所以原方程无解；
（2）当
，即
时，方程①的根为：，
所以
或
，
所以
或
，
所以存在实数，使得方程恰有4个不同的实根；
（3）当
时，方程①的根为
或
，
所以
或
，解得：
或
或
，
所以存在实数，使得方程恰有5个不同的实根；
（4）当
时，方程①的根：
，
，
考察函数
的图象可得：原方程有8个根；
（5）当
时，方程①的根：
，
考察函数的图象可得：原方程有2个根；
存在实数
，使得方程恰有2个不同的实根；
故选：A
练习册系列答案
阅读快车系列答案
相关题目
