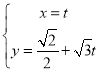题目内容
【题目】如图,某隧道设计为双向四车道,车道总宽为![]() ,要求通行车辆限高
,要求通行车辆限高![]() ,隧道全长为
,隧道全长为![]() ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.
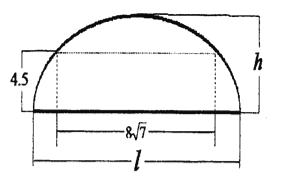
(1)若最大拱高![]() 为
为![]() ,则隧道设计的拱宽
,则隧道设计的拱宽![]() 是多少?
是多少?
(2)若最大拱高![]() 不小于
不小于![]() ,则应如何设计拱高
,则应如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?
(注: 1.半个椭圆的面积公式为![]() ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积![]() 隧道长)
隧道长)
【答案】(1)32![]() ;(2)当拱高为
;(2)当拱高为![]() ,拱宽为
,拱宽为![]() 时,土方工程量最小.
时,土方工程量最小.
【解析】
试题分析:本题是椭圆的实际应用题,考查利用椭圆标准方程解应用题.(1)以车道中点为原点,建立直角坐标系,则![]() 在椭圆上,这时椭圆方程可设为
在椭圆上,这时椭圆方程可设为![]() ,由
,由![]() 及
及![]() 点坐标可求得椭圆中的
点坐标可求得椭圆中的![]() ,从而得结论;(2)隧道的土方工程量最小即半椭圆的面积最小,即椭圆的面积为
,从而得结论;(2)隧道的土方工程量最小即半椭圆的面积最小,即椭圆的面积为![]() 最小,利用标准方程及基本不等式可求得
最小,利用标准方程及基本不等式可求得![]() 的最小值.
的最小值.
试题解析:(1)以车道中点为原点,建立直角坐标系,则![]() ,
,
设椭圆的方程为![]() ,则
,则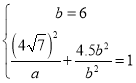 解之得:
解之得:![]() ,
,
此时![]() .
.
(2)由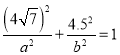 ,可知
,可知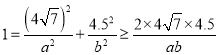 ,
,
故![]() ,所以
,所以![]() ,
,
当且仅当![]() 时取等号,
时取等号,
答:当拱高为![]() ,拱宽为
,拱宽为![]() 时,土方工程量最小.
时,土方工程量最小.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目