题目内容
对于n个向量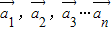
，若存在n个不全为零的实数k1，k2，…kn，使得：
成立，则称向量
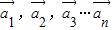是线性相关的．按此规定，能使向量
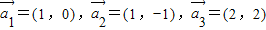是线性相关的实数为k1，k2，k3，则k1+4k3= ．
【答案】分析：观察已知条件可得
，把向量的坐标代入，根据向量相等的条件可得
联立方程可得
解答：解：由题意得
则（k1，0）+（k2，-k2）+（2k3，2k3）=（0，0）
两式相加可得k1+4k3=0
故答案为：0
点评：本题以新定义为载体，考查向量加法坐标表示的基本运算及向量相等的条件，建立方程后，利用整体思想求解结果．
，把向量的坐标代入，根据向量相等的条件可得联立方程可得解答：解：由题意得
则（k1，0）+（k2，-k2）+（2k3，2k3）=（0，0）
两式相加可得k1+4k3=0
故答案为：0
点评：本题以新定义为载体，考查向量加法坐标表示的基本运算及向量相等的条件，建立方程后，利用整体思想求解结果．
练习册系列答案
相关题目
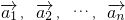，若存在n个不全为零的实数k1，k2，…，kn，使得
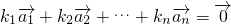，则称
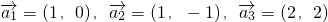线性相关，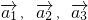
的相关系数分别为k1，k2，k3，则k1：k2：k3=________．
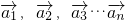，若存在n个不全为零的实数k1，k2，…kn，使得：
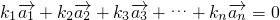成立，则称向量
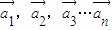，若存在n个不全为零的实数k1，k2，…kn，使得：
成立，则称向量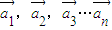
是线性相关的．按此规定，能使向量
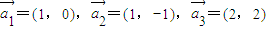是线性相关的实数为k1，k2，k3，则k1+4k3= ．