题目内容
如图椭圆 的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上.
的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上.(Ⅰ)求椭圆的离心率;
(Ⅱ)若平行四边形OCED的面积为
 ,求椭圆的方程.
,求椭圆的方程.
【答案】分析:(I)根据题意可知AB的斜率,进而根据点斜式表示出直线CD的方程,代入椭圆方程,进而可表示出CD的中点的坐标,则E点的坐标可得,代入椭圆方程即可求得a和c的关系式求得离心率e.
(II)先设直线CD的方程,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得c值,从而解决问题.
解答:解:(Ⅰ)∵焦点为F(c,0),AB斜率为 ,故CD方程为y=
,故CD方程为y= (x-c).与椭圆联立后消去y得2x2-2cx-b2=0.
(x-c).与椭圆联立后消去y得2x2-2cx-b2=0.
∵CD的中点为G( ,-
,- ),点E(c,-
),点E(c,- )在椭圆上,
)在椭圆上,
∴将E(c,- )代入椭圆方程并整理得2c2=a2,
)代入椭圆方程并整理得2c2=a2,
∴e= .
.
(Ⅱ)由(Ⅰ)知CD的方程为y= (x-c),b=c,a=
(x-c),b=c,a= c.
c.
与椭圆联立消去y得2x2-2cx-c2=0.
∵平行四边形OCED的面积为:
S=c|yC-yD|= c
c
= c
c ,
,
∴c= ,a=2,b=
,a=2,b= .
.
故椭圆方程为 .
.
点评:本题主要考查了椭圆的简单性质,考查了学生综合运用基础知识的能力.
(II)先设直线CD的方程,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得c值,从而解决问题.
解答:解:(Ⅰ)∵焦点为F(c,0),AB斜率为
 ,故CD方程为y=
,故CD方程为y= (x-c).与椭圆联立后消去y得2x2-2cx-b2=0.
(x-c).与椭圆联立后消去y得2x2-2cx-b2=0.∵CD的中点为G(
 ,-
,- ),点E(c,-
),点E(c,- )在椭圆上,
)在椭圆上,∴将E(c,-
 )代入椭圆方程并整理得2c2=a2,
)代入椭圆方程并整理得2c2=a2,∴e=
 .
.(Ⅱ)由(Ⅰ)知CD的方程为y=
 (x-c),b=c,a=
(x-c),b=c,a= c.
c.与椭圆联立消去y得2x2-2cx-c2=0.
∵平行四边形OCED的面积为:
S=c|yC-yD|=
 c
c
=
 c
c ,
,∴c=
 ,a=2,b=
,a=2,b= .
.故椭圆方程为
 .
.点评:本题主要考查了椭圆的简单性质,考查了学生综合运用基础知识的能力.

练习册系列答案
相关题目
 的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
 , 求椭圆的方程.
, 求椭圆的方程.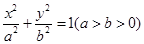 的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。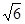 , 求椭圆的方程.
, 求椭圆的方程.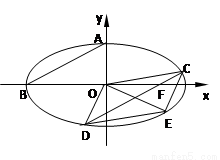
 如图椭圆
如图椭圆 的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上.
的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上. ,求椭圆的方程.
,求椭圆的方程. 的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上.
的上顶点为A,左顶点为B,F为右焦点,过F作平行与AB的直线交椭圆于C、D两点.作平行四边形OCED,E恰在椭圆上. ,求椭圆的方程.
,求椭圆的方程.