Question

(本小题满分12分)

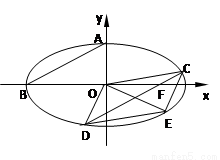
如图椭圆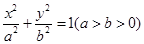的上顶点为A，左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。

（1）求椭圆的离心率；

（2）若平行四边形OCED的面积为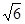, 求椭圆的方程.

 

Answer 1

【答案】

（1）；（2）

【解析】

试题分析：(1) ∵焦点为F(c, 0), AB斜率为, 故CD方程为y=(x－c). 于椭圆联立后消去y得2x²－2cx－b²=0. ∵CD的中点为G(), 点E(c, －)在椭圆上,

∴将E(c, －)代入椭圆方程并整理得2c²=a², ∴e =.

(2)由(Ⅰ)知CD的方程为y=(x－c),  b=c, a=c.

与椭圆联立消去y得2x²－2cx－c²=0.

∵平行四边形OCED的面积为S=c|y_C－y_D|=c

=c, ∴c=, a=2, b=. 故椭圆方程为。

考点：本题考查椭圆的简单性质。

点评：求椭圆的离心率是常见题型，其主要思路是：找出a、b、c的一个关系式即可。此题就是根据点斜式表示出直线CD的方程，代入椭圆方程，进而可表示出CD的中点的坐标，则E点的坐标可得，代入椭圆方程即可求得a、b和c的关系式求得离心率e．