题目内容
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的左右焦点,过点
分别是椭圆的左右焦点,过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,且
两点,且![]() 的周长为12.
的周长为12.
(Ⅰ)求椭圆![]() 的方程
的方程
(Ⅱ)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形若存在,求点
为底边的等腰三角形若存在,求点![]() 横坐标的取值范围,若不存在,请说明理由.
横坐标的取值范围,若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]()
【解析】
(Ⅰ)由椭圆的离心率为![]() 和
和![]() 的周长为12可得
的周长为12可得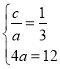 ,可求椭圆方程.
,可求椭圆方程.
(Ⅱ)![]() 的中点为
的中点为![]() ,由条件有
,由条件有![]() ,即
,即![]() ,设
,设![]() ,用直线
,用直线![]() 的斜率把
的斜率把![]() 表示出来,可求解其范围.
表示出来,可求解其范围.
(1)由题意可得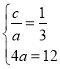 ,所以
,所以![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .假设存在点
.假设存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,则
为底边的等腰三角形,则![]() .由
.由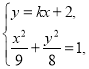 得
得![]() ,
,
故![]() ,所以
,所以![]() ,
,![]()
因为![]() ,所以
,所以![]() ,即
,即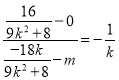 ,所以
,所以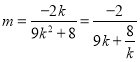
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]()
综上:m取值范围是![]() 或
或![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目