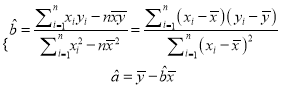题目内容
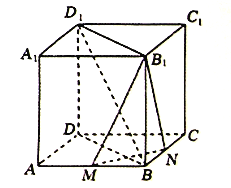
【题目】若图,在正方体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是存在一点
上是存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)证明过程见解析;(2) ![]()
【解析】试题分析:(1)连接![]() ,由正方形性质得
,由正方形性质得![]() ,又由正方体
,又由正方体![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,易得
的中点,易得![]() ,则
,则![]() ,
, ![]() ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得![]() 平面
平面![]() ,进而由面面垂直的判定定理,可得平面
,进而由面面垂直的判定定理,可得平面![]() 平面
平面![]() ;(2)设
;(2)设![]() 与
与![]() 的交点是
的交点是![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,由线面平行的性质定理,我们易由
,由线面平行的性质定理,我们易由![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得
,得![]() ,再由平行线分线段成比例定理,得到线段
,再由平行线分线段成比例定理,得到线段![]() 与
与![]() 的比.
的比.
试题解析:(1)证明:连接![]() ,则
,则![]() ,又
,又![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() ,因为
,因为![]() 是正方体,
是正方体,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() 。
。
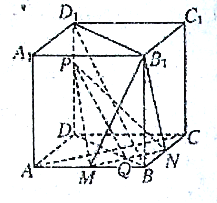
(2)设![]() 与
与![]() 的交点是
的交点是![]() ,连接
,连接![]() ,
,
因为![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()

练习册系列答案
相关题目
【题目】陕西省洛川地处北纬35°-36°,东经109°,昼夜温差![]() ,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用
,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用![]() (万元)与销售额
(万元)与销售额![]() (万元)之间有下面对应数据:
(万元)之间有下面对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)假设![]() 与
与![]() 之间线性相关,求回归直线方程;
之间线性相关,求回归直线方程;
(2)预测广告和包装费用为10(万元)时销售额是多少?
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)已知产量![]() 和能耗
和能耗![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: