题目内容
选做题(A)选修4-1:几何证明选讲
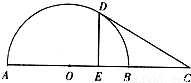
如图,AB是半圆O的直径,延长AB到C,使
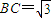 ,CD切半圆于点D,DE⊥AB,垂足为E,若AE:EB=3:1,求DE的长.
,CD切半圆于点D,DE⊥AB,垂足为E,若AE:EB=3:1,求DE的长.(B)选修4-2:矩阵与变换
在平面直角坐标系xOy中,直线y=kx在矩阵
 对应的变换下得到的直线经过点P(4,1),求实数k的值.
对应的变换下得到的直线经过点P(4,1),求实数k的值.(C)选修4-4:坐标系与参数方程
在极坐标系中,已知圆ρ=asinθ(a>0)与直线
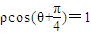 相切,求实数a的值.
相切,求实数a的值.(D)选修4-5:不等式选讲
已知a,b,c满足abc=1,求证:(a+2)(b+2)(c+2)≥27.
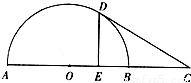
【答案】分析:(A)连接OD、BD,由题目中条件知:“DE⊥AB,垂足为E,且E是OB的中点”可得三角形BOD是等边三角形,设圆的半径为R,再在直角三角形OCD中,可得CD的长,最后根据题中圆的切线条件再依据切割线定理求得DE的长.
(B)设变换T: →
→ ,直线y=kx上任意一点(x,y),(x′,y′)是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.
,直线y=kx上任意一点(x,y),(x′,y′)是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.
(C)先圆ρ=acosθ与直线 ,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
(D):将(a+2)(b+2)(c+2)展开,再利用基本不等式结合条件abc=1,即可证得.
解答: 解:(A)连接OD,
解:(A)连接OD,
∵DE⊥AB,垂足为E,且AE:EB=3:1得E是OB的中点
∴可得等腰三角形BOD是等边三角形,
在直角三角形OCD中,∠COD=60°,设圆的半径为R,
∴可得CD= OD=
OD= R,
R,
∵CD是圆O的切线,∴由切割线定理得,
∴CD2=CB×CA,
即3R2= ×(
×( +2R)
+2R)
∴R= ,
,
∴DE= OE=
OE= ×
× =
= ;
;
(B):设变换 T: →
→ ,
,
则 =
=
 ,(5分)
,(5分)
即 代入直线y=kx得y'=kx',
代入直线y=kx得y'=kx',
将点P(4,1)代入,
得k= .
.
(C):p2=apcosθ,圆ρ=acosθ的普通方程为:x2+y2=ax,(x-a)2+y2=a2,
直线 的普通方程为:x-y-
的普通方程为:x-y- =0,
=0,
又圆与直线相切,所以 =a,解得:a=-
=a,解得:a=- ±2.
±2.
∵a>0,∴a=- +2.
+2.
(D):(a+2)(b+2)(c+2)
=abc+2(ab+bc+ca)+4(a+b+c)+8
≥1+2×3 +4×3
+4×3 +8
+8
=27,当且仅当a=b=c时等号成立.
点评:本题主要考查二阶矩阵的变换,简单曲线的极坐标方程,不等式的证明等.考查运算求解能力.
(B)设变换T:
 →
→ ,直线y=kx上任意一点(x,y),(x′,y′)是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.
,直线y=kx上任意一点(x,y),(x′,y′)是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.(C)先圆ρ=acosθ与直线
 ,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.(D):将(a+2)(b+2)(c+2)展开,再利用基本不等式结合条件abc=1,即可证得.
解答:
 解:(A)连接OD,
解:(A)连接OD,∵DE⊥AB,垂足为E,且AE:EB=3:1得E是OB的中点
∴可得等腰三角形BOD是等边三角形,
在直角三角形OCD中,∠COD=60°,设圆的半径为R,
∴可得CD=
 OD=
OD= R,
R,∵CD是圆O的切线,∴由切割线定理得,
∴CD2=CB×CA,
即3R2=
 ×(
×( +2R)
+2R)∴R=
 ,
,∴DE=
 OE=
OE= ×
× =
= ;
;(B):设变换 T:
 →
→ ,
,则
 =
=
 ,(5分)
,(5分)即
 代入直线y=kx得y'=kx',
代入直线y=kx得y'=kx',将点P(4,1)代入,
得k=
 .
.(C):p2=apcosθ,圆ρ=acosθ的普通方程为:x2+y2=ax,(x-a)2+y2=a2,
直线
 的普通方程为:x-y-
的普通方程为:x-y- =0,
=0,又圆与直线相切,所以
 =a,解得:a=-
=a,解得:a=- ±2.
±2.∵a>0,∴a=-
 +2.
+2.(D):(a+2)(b+2)(c+2)
=abc+2(ab+bc+ca)+4(a+b+c)+8
≥1+2×3
 +4×3
+4×3 +8
+8=27,当且仅当a=b=c时等号成立.
点评:本题主要考查二阶矩阵的变换,简单曲线的极坐标方程,不等式的证明等.考查运算求解能力.

练习册系列答案
相关题目
 (2012•江苏一模)选做题
(2012•江苏一模)选做题
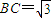 ,CD切半圆于点D,DE⊥AB,垂足为E,若AE:EB=3:1,求DE的长.
,CD切半圆于点D,DE⊥AB,垂足为E,若AE:EB=3:1,求DE的长. 对应的变换下得到的直线经过点P(4,1),求实数k的值.
对应的变换下得到的直线经过点P(4,1),求实数k的值.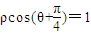 相切,求实数a的值.
相切,求实数a的值.