Question

过点P（2，－1）作直线l交曲线xy=1于A,B两点,求AB中点M的轨迹方程.

Answer 1

解:设AB中点M(x₀,y₀),l的倾斜角为α,则l的参数方程为

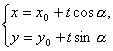(t为参数),

代入xy=1,即(tcosα+x₀)(tsinα+y₀)=1

t²sinαcosα+(y₀cosα+x₀sinα)t+x₀y₀-1=0.

由于M(x₀,y₀)为弦中点,则t₁+t₂=0.

∴y₀cosα+x₀sinα=0y₀+x₀=0.

将=tanα=k=代入,则y₀+x₀=02xy+x-2y=0为所求.