题目内容
已知函数y=lg(x2+1-x),求其定义域,并判断其奇偶性、单调性.?
解:注意到![]() +x=
+x=![]() ,即有lg(
,即有lg(![]() -x)=-lg(
-x)=-lg(![]() +x),从而f(-x)=lg(
+x),从而f(-x)=lg(![]() +x)=-lg(
+x)=-lg(![]() -x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
-x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
由题意![]() -x>0,解得x∈R,即定义域为R.
-x>0,解得x∈R,即定义域为R.
又f(-x)=lg[![]() -(-x)]=lg(
-(-x)]=lg(![]() +x)?
+x)?
=lg![]() =lg(
=lg(![]() -x) -1
-x) -1
=-lg(![]() -x)=-f(x).
-x)=-f(x).
∴y=lg(![]() -x)是奇函数.
-x)是奇函数.
任取x 1、x 2∈(0,+∞)且x 1<x 2,
则![]() <
<![]()
![]()
![]() +x 1<
+x 1<![]() +x 2
+x 2
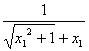 >
>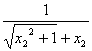 ,
,
即有![]() -x 1>
-x 1>![]() -x2>0,
-x2>0,
∴lg(![]() -x 1)>lg(
-x 1)>lg(![]() -x 2),
-x 2),
即f(x 1)>f(x 2)成立.?
∴f(x)在(0,+∞)上为减函数.?
又f(x)是定义在R上的奇函数,
故f(x)在(-∞,0)上也为减函数.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
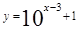 (x≥3)
(B)
(x≥3)
(B) 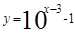 (x∈R) (D)
(x∈R) (D) 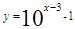 (x≥3)
(x≥3)