题目内容
已知a为实数,f(x)=(x2-4)(x-a),
(Ⅰ)求导数f′(x);
(Ⅱ)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(Ⅲ)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
(Ⅰ)求导数f′(x);
(Ⅱ)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(Ⅲ)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
解:(Ⅰ)由原式得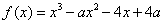 ,
,
∴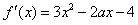 ;
;
(Ⅱ)由f′(-1)=0,得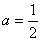 ,
,
此时有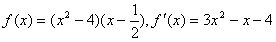 ,
,
由f′(-1)=0得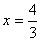 或x=-1,
或x=-1,
又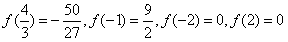 ,
,
所以f(x)在[--2,2]上的最大值为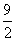 ,最小值为
,最小值为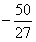 。
。
(Ⅲ)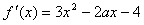 的图象为开口向上且过点(0,-4)的抛物线,
的图象为开口向上且过点(0,-4)的抛物线,
由条件得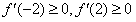 ,即
,即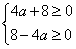 ,
,
∴-2≤a≤2,
所以a的取值范围为[-2,2]。
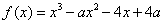 ,
, ∴
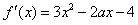 ;
;(Ⅱ)由f′(-1)=0,得
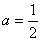 ,
,此时有
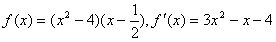 ,
,由f′(-1)=0得
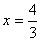 或x=-1,
或x=-1,又
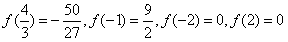 ,
,所以f(x)在[--2,2]上的最大值为
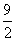 ,最小值为
,最小值为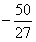 。
。(Ⅲ)
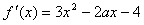 的图象为开口向上且过点(0,-4)的抛物线,
的图象为开口向上且过点(0,-4)的抛物线,由条件得
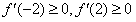 ,即
,即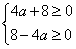 ,
,∴-2≤a≤2,
所以a的取值范围为[-2,2]。

练习册系列答案
相关题目