题目内容
13.已知命题p:关于x的方程a2x2-ax-2=0在x∈[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0.(1)若“p且q”是真命题,求实数a的取值范围;
(2)若“p或q”是假命题,求实数a的取值范围.
分析 先求出p,q为真时的a的范围,如果“p且q”为真命题,“p,q”也为真命题,则“p或q”为假命题.,“p,q”都假,即可求解.
解答 解:对于命题p:由a2x2-ax-2=0在[-1,1]上有解,
当a=0时,不符合题意;
当a≠0时,方程可化为:(ax-2)(ax+1)=0,
解得:x=$\frac{2}{a}$,或x=-$\frac{1}{a}$,
∵x∈[-1,1],
∴-1≤$\frac{2}{a}$≤1或-1≤-$\frac{1}{a}$≤1,
解得:a≥2或a≤-2
对于命题q:由只有一个实数x满足不等式x2+2ax+2a≤0
得抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0
∴a=0或a=2
(1)若“p且q”是真命题,则a=2,
(2)若“p或q”是假命题,则-2<a<2且a≠0.
点评 由简单命题和逻辑连接词构成的复合命题的真假可以用真值表来判断,反之根据复合命题的真假也可以判断简单命题的真假.假若p且q真,则p 真,q也真;若p或q真,则p,q至少有一个真;若p且q假,则p,q都假,本题属于基础题.

练习册系列答案
相关题目
3.下列语句是真命题的是( )
| A. | 所有的实数x都能使x+$\frac{1}{x}$≥2成立 | |
| B. | 存在一个实数x使不等式x2-2x+3<0成立 | |
| C. | 如果x、y 是实数,那么“xy>0”是“|x+y|=|x|+|y|”的充分但不必要条件 | |
| D. | 命题甲:“a、b、c”成等差数列”是命题乙:“$\frac{a}{b}+\frac{c}{b}$=2”的充要条件 |
5.若x+y+z=0,则x3+y3+z3=( )
| A. | 0 | B. | x2y+y2z+z2x | C. | x2+y2+z2 | D. | 3xyz |
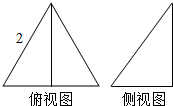 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.