题目内容
如图,侧棱垂直底面的三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)试求三棱锥![]() 的体积
的体积![]() 取得最大值时的
取得最大值时的![]() 值;
值;
(Ⅲ)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,试求实数
,试求实数![]() 的值.
的值.

解:(Ⅰ)证法一:∵![]() 面
面![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,∴四边形
,∴四边形![]() 是正方形,
是正方形,
∴![]() . ………1分
. ………1分
∵![]() ,
,
∴![]() . ………2分
. ………2分
又∵![]() , ∴
, ∴![]() . ………3分
. ………3分
∵![]() ,
,
∴![]() . ………4分
. ………4分
证法二:∵![]() 面
面![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,
,
∴分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系.……1分
轴建立空间直角坐标系.……1分
则![]() ,
,
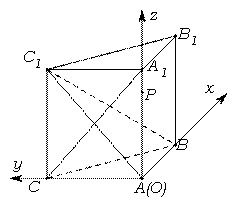
![]() ,
,
∴![]() , …2分
, …2分
∴![]() . …3分
. …3分
又∵![]()
∴![]() . …4分
. …4分
证法三:∵![]() 面
面![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,
,
∴分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系.……1分
轴建立空间直角坐标系.……1分
则![]() ,
,
![]() .
.

设平面![]() 的法向量
的法向量![]() ,
,
则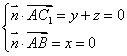 ,解得
,解得![]() .
.
令![]() ,则
,则![]() , ……3分
, ……3分
∵![]() , ∴
, ∴![]() . ……4分
. ……4分
(Ⅱ)∵![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离
的距离
∴![]() , …5分
, …5分
![]() ,
,
令![]() ,得
,得![]() (舍去)或
(舍去)或![]() ,
,
列表,得
|
| 1 |
| |
|
| + | 0 | - |
|
| 递增 | 极大值 | 递减 |
∴当![]() 时,
时,![]() . …8分
. …8分
(Ⅲ)分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,

![]() ,
,
![]() ,
,![]() . ……9分
. ……9分
设平面![]() 的法向量
的法向量![]() ,
,
则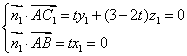 ,解得
,解得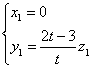 ,
,
令![]() ,则
,则![]() . …10分
. …10分
设平面![]() 的法向量
的法向量![]() ,
,
则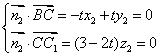 .
.
由于![]() ,所以解得
,所以解得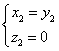 .
.
令![]() ,则
,则![]() . …11分
. …11分
设二面角![]() 的平面角为
的平面角为![]() ,
,
则有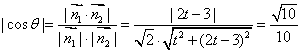 .
.
化简得![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
所以当![]() 时,二面角
时,二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() . …13分
. …13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
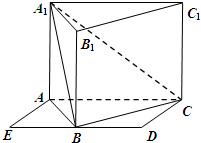 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.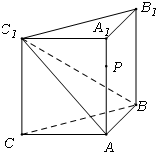 如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.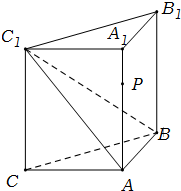 (2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.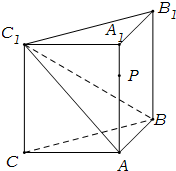 (2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.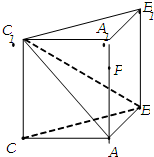 (2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
(2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).