题目内容
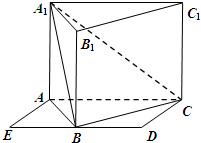 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.(Ⅰ)求证:平面A1BC⊥平面A1ABB1.
(Ⅱ)求二面角A-A1C-B的大小.
分析:(1)先证AB⊥BC,再由直三棱柱的定义证明AA1⊥BC,从而得到直线垂直于平面,根据面与面垂直的判定定理得到结论.
(2)建立坐标系,写出要用的点的坐标,在两个平面上,各自写出两个向量,设出平面的法向量.根据向量垂直的充要条件,得到平面的法向量,根据法向量之间角的关系得到结果.
(2)建立坐标系,写出要用的点的坐标,在两个平面上,各自写出两个向量,设出平面的法向量.根据向量垂直的充要条件,得到平面的法向量,根据法向量之间角的关系得到结果.
解答: 解:(Ⅰ)法一、在平行四边形ACDE中,
解:(Ⅰ)法一、在平行四边形ACDE中,
∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴∠ABE=60°,∠CBD=30°,
从而∠ABC=90°,即AB⊥BC.
又AA1⊥面ABC,BC?面ABC
∴AA1⊥BC,而AA1∩AB=A,
∴⊥平面A1ABC1.
∵BC?平面A1BC
∴平面A1BC⊥平面A1ABB1
(Ⅱ)由题意知建立坐标系,以A为原点,AC所在的直线为y轴,AA1为z轴建立坐标系,
A(0,0,0),C(0,4,0),A1(0,0,4),B(
,1,0)
设出两个平面的法向量分别是
=(x,y,z),
(a,b,c)
∵
•
=0,
•
=0,
•
=0,
•
=0,
∴
=(1,0,0),
=(
,1,1),
∴cosθ=
=
∴二面角A-A1C-B的大小为arccos
 解:(Ⅰ)法一、在平行四边形ACDE中,
解:(Ⅰ)法一、在平行四边形ACDE中,∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴∠ABE=60°,∠CBD=30°,
从而∠ABC=90°,即AB⊥BC.
又AA1⊥面ABC,BC?面ABC
∴AA1⊥BC,而AA1∩AB=A,
∴⊥平面A1ABC1.
∵BC?平面A1BC
∴平面A1BC⊥平面A1ABB1
(Ⅱ)由题意知建立坐标系,以A为原点,AC所在的直线为y轴,AA1为z轴建立坐标系,
A(0,0,0),C(0,4,0),A1(0,0,4),B(
| 3 |
设出两个平面的法向量分别是
| m |
| n |
∵
| m |
| AA1 |
| m |
| AC |
| n |
| CB |
| n |
| A1C |
∴
| m |
| n |
| 3 |
∴cosθ=
| ||
|
| ||
| 5 |
∴二面角A-A1C-B的大小为arccos
| ||
| 5 |
点评:这是一个典型的立体几何题目,是高考题中常出现的问题,有边角关系的证明,有用空间向量求解关于面面角的问题,解题时主要在建立坐标系,写出点的坐标,用向量法解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
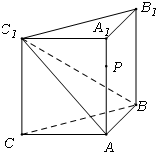 如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.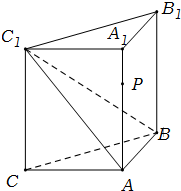 (2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.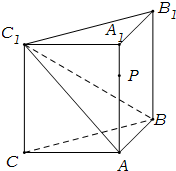 (2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.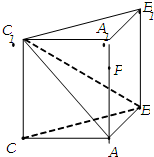 (2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
(2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).