题目内容
已知等差数列an满足:a3=7,a5+a7=26,令 ,则数列bn的前n项和Tn=________.
,则数列bn的前n项和Tn=________.

分析:根据所给的等差数列的三个连续奇数项,得到数列的公差,写出数列的通项,构造新数列,整理出可以应用裂项求和的形式,得到结果.
解答:∵等差数列an满足:a3=7,a5+a7=26,
∴a3+a5+a7=33,
∴a5=11
∴d=
 =2
=2∴an=2n+1,
∴

∴4

=
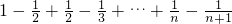 =
=
∴

故答案为:

点评:本题考查数列的求和和数列的通项,本题解题的关键是构造出新函数,看出数列的通项符合裂项求和的形式.

练习册系列答案
相关题目