题目内容
设函数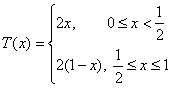
(1)求函数![]() 和
和![]() 的解析式;
的解析式;
(2)是否存在非负实数![]() ,使得
,使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;

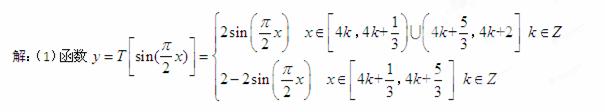
函数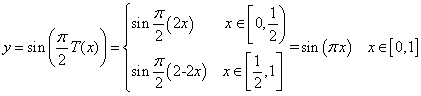 ……4分
……4分
(2)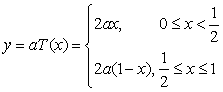 ,
,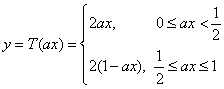 ……6分
……6分
当![]() 时,则有
时,则有![]() 恒成立.
恒成立.
当![]() 时,当且仅当
时,当且仅当![]() 时有
时有![]() 恒成立.
恒成立.
综上可知当![]() 或
或![]() 时,
时,![]() 恒成立;………………………8分
恒成立;………………………8分
(3)① 当![]() 时,对于任意的正整数
时,对于任意的正整数![]() ,都有
,都有![]()
故有![]() …13分
…13分
 解得
解得![]() , 若将这些根从小到大排列组成数列
, 若将这些根从小到大排列组成数列![]() ,
,
由此可得![]()
![]() .……………………17分
.……………………17分
故数列![]() 所有
所有![]() 项的和为:
项的和为:
![]()
![]()
![]() .……18分
.……18分

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目