题目内容
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求∠C;
(2)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长;
,求△ABC的周长;
(3)若c= ![]() ,求△ABC的周长的取值范围.
,求△ABC的周长的取值范围.
【答案】
(1)解: 2cosC(acosB+bcosA)=c.
由正弦定理:可得:2cosC(sinAcosB+sinBcosA)=sinC
即2cosCsinC=sinC
∵0<C<π,sinC≠0,
∴cosC= ![]()
∴C= ![]() .
.
(2)由△ABC的面积为 ![]() ,即
,即 ![]() absinC=
absinC= ![]() ,
,
∵C= ![]() .
.
∴ab=6.
由c= ![]() ,余弦定理:c2=a2+b2﹣2abcosC.
,余弦定理:c2=a2+b2﹣2abcosC.
可得:a2+b2﹣ab=7.
即(a+b)2=7+3ab=25.
∴a+b=5.
那么△ABC的周长为:a+b+c=5 ![]() .
.
(3)∵c= ![]() ,C=
,C= ![]() .
.
正弦定理:a= ![]() ,b=
,b= ![]()
△ABC的周长:a+b+c=2sinA+2sinB+ ![]() .
.
∵C= ![]() ,A+B+C=π
,A+B+C=π
∴B= ![]() .
.
则a+b=2sinA+2sinB=2sinA+2sin( ![]() )=3sinA+
)=3sinA+ ![]() cosA=2
cosA=2 ![]() sin(A+
sin(A+ ![]() )
)
∵0<A ![]() ,
,
∴ ![]() <A+
<A+ ![]() ,
,
∴ ![]() <2
<2 ![]() sin(A+
sin(A+ ![]() )
) ![]() .
.
即 ![]() <a+b
<a+b ![]()
∴△ABC的周长的取值范围为:(2 ![]() ,4
,4 ![]() ].
].
【解析】1、由正弦定理:可得:2cosC(sinAcosB+sinBcosA)=sinC,∵0<C<π,sinC≠0,∴cosC= ![]() ∴C=
∴C= ![]() .
.
2、由△ABC的面积为 ![]() ,即
,即 ![]() 可得ab=6.由c=
可得ab=6.由c= ![]() ,余弦定理可得a+b=5,所以△ABC的周长为:a+b+c=5 +
,余弦定理可得a+b=5,所以△ABC的周长为:a+b+c=5 + ![]() 。
。
3、根据题意由正玄定理可得,![]() ABC的周长:a+b+c=2sinA+2sinB+
ABC的周长:a+b+c=2sinA+2sinB+ ![]() ,∵C=
,∵C= ![]() ,A+B+C=π ,∴B=
,A+B+C=π ,∴B= ![]() A 得到a+b=2sinA+2sinB=2sinA+2sin
A 得到a+b=2sinA+2sinB=2sinA+2sin![]() =3sinA+
=3sinA+ ![]() cosA=2
cosA=2 ![]() sin
sin![]() .∵0<A <
.∵0<A < ![]() ,∴
,∴ ![]() <A+
<A+ ![]() <
< ![]() ,即
,即 ![]() <a+b ≤ 2
<a+b ≤ 2![]() ,得到△ABC的周长的取值范围为:(2
,得到△ABC的周长的取值范围为:(2![]() ,4
,4 ![]() ].
].
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”. 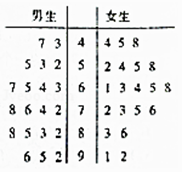
(1)完成下面2×2列联表,
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(2)判断是否有90%的把握认为“空间想象能力突出”与性别有关;
(3)从“空间想象能力突出”的同学中随机选取男生2名、女生2名,记其中成绩超过90分的人数为ξ,求随机变量ξ的分布列和数学期望. 下面公式及临界值表仅供参考: ![]()
P(X2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |