题目内容
对于命题P:存在一个常数M,使得不等式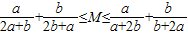 对任意正数a,b恒成立.
对任意正数a,b恒成立.(1)试猜想常数M的值,并予以证明;
(2)类比命题P,某同学猜想了正确命题Q:存在一个常数M,使得不等式
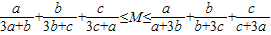 对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).
对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).
【答案】分析:(1)令a=b,得 ,故
,故 . 先用分析法证明
. 先用分析法证明  ,同理可证明
,同理可证明 ,命题得证.
,命题得证.
(2)利用类比推理可得,存在一个常数M,使得不等式 对任意正数a,b,c,d恒成立.
对任意正数a,b,c,d恒成立.
解答:解:(1)令a=b,得 ,故
,故 . 先证明
. 先证明 :
:
∵a>0,b>0,要证上式,只要证3a(2b+a)+3b(2a+b)≤2(2a+b)(2b+a),
即证a2+b2≥2ab,即证(a-b)2≥0,这显然成立.∴ .
.
再证明 :
:
∵a>0,b>0,要证上式,只要证3a(2a+b)+3b(2b+a)≥2(a+2b)(b+2a),
即证a2+b2≥2ab,即证(a-b)2≥0,这显然成立.∴ .
.
(2)存在一个常数M,使得不等式
对任意正数a,b,c,d恒成立.
点评:办呢题考查用分析法证明不等式,类比推理,找出M的值,是解题的突破口.
 ,故
,故 . 先用分析法证明
. 先用分析法证明  ,同理可证明
,同理可证明 ,命题得证.
,命题得证.(2)利用类比推理可得,存在一个常数M,使得不等式
 对任意正数a,b,c,d恒成立.
对任意正数a,b,c,d恒成立.解答:解:(1)令a=b,得
 ,故
,故 . 先证明
. 先证明 :
:∵a>0,b>0,要证上式,只要证3a(2b+a)+3b(2a+b)≤2(2a+b)(2b+a),
即证a2+b2≥2ab,即证(a-b)2≥0,这显然成立.∴
 .
.再证明
 :
:∵a>0,b>0,要证上式,只要证3a(2a+b)+3b(2b+a)≥2(a+2b)(b+2a),
即证a2+b2≥2ab,即证(a-b)2≥0,这显然成立.∴
 .
.(2)存在一个常数M,使得不等式

对任意正数a,b,c,d恒成立.
点评:办呢题考查用分析法证明不等式,类比推理,找出M的值,是解题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
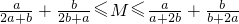 对任意正数a,b恒成立.
对任意正数a,b恒成立.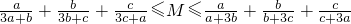 对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).
对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).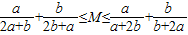 对任意正数a,b恒成立.
对任意正数a,b恒成立.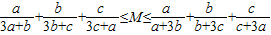 对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).
对任意正数a,b,c恒成立,观察命题P与命题Q的规律,请猜想与正数a,b,c,d相关的正确命题(不需要证明).