Question

【题目】△ABC的内角A，B，C的对边分别为，已知且．

(1)求角；

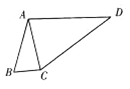
(2)如图，D为△ABC外一点，若在平面四边形ABCD中，，求△ACD面积的最大值．

Answer 1

【答案】(1) ;(2) 面积的最大值为.

【解析】

（1）由已知及正弦定理可得：2cosB=，进而可求cosB=，由B为三角形内角，可得B的值；

（2）在△ABC中，由余弦定理可得b的值，由B=，根据余弦定理，均值定理可得：ADCD≤24+12，根据三角形面积公式即可计算得解．

（1）由题意知：

由正弦定理知：

在中，，

所以，所以，B为内角，

所以.

（2）在中，由余弦定理知：

，

所以，

在中，，由余弦定理知，

即，

由均值定理知，当且仅当“”时取等号

所以，即；

，

所以面积的最大值为